Soru Çözümü
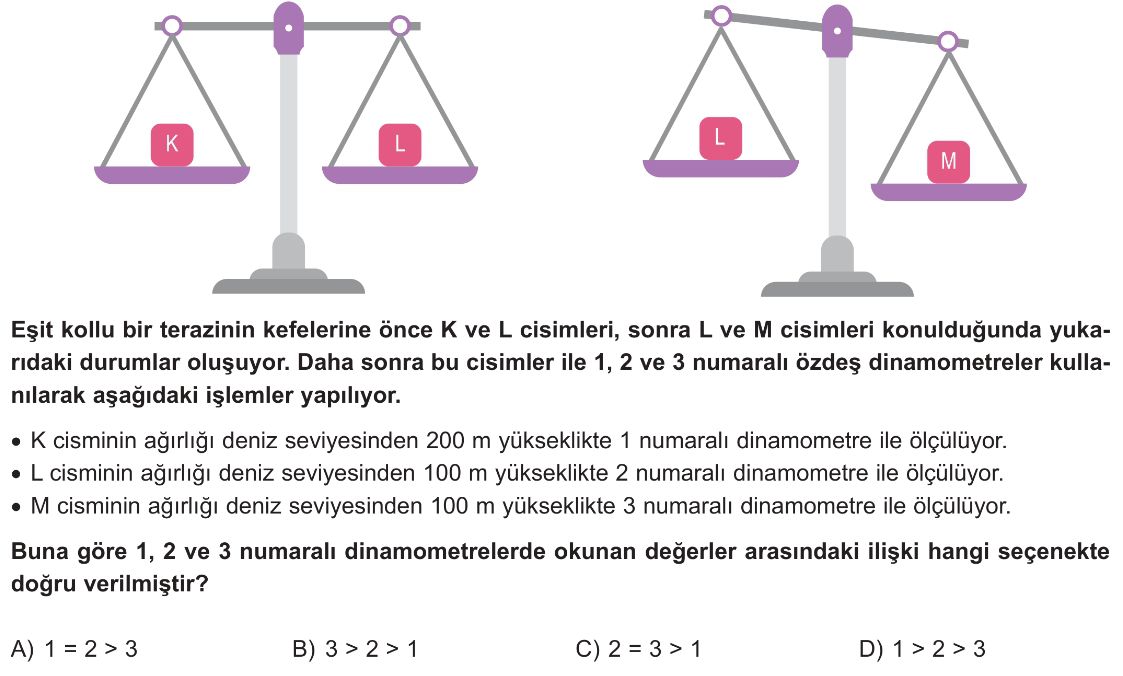
- İlk terazi dengede olduğundan, K ve L cisimlerinin kütleleri eşittir: $m_K = m_L$.
- İkinci terazi dengede olduğundan, L ve M cisimlerinin kütleleri eşittir: $m_L = m_M$.
- Bu durumda, üç cismin kütleleri birbirine eşittir: $m_K = m_L = m_M$.
- Ağırlık, kütle ile yer çekimi ivmesinin çarpımıdır ($W = m \cdot g$). Yer çekimi ivmesi, deniz seviyesinden yükseklik arttıkça azalır. Yani, $100 m$ yükseklikteki yer çekimi ivmesi, $200 m$ yüksekliktekinden daha büyüktür ($g_{100m} > g_{200m}$).
- 1 numaralı dinamometre K cisminin ağırlığını $200 m$ yükseklikte ölçer: $W_1 = m_K \cdot g_{200m}$.
- 2 numaralı dinamometre L cisminin ağırlığını $100 m$ yükseklikte ölçer: $W_2 = m_L \cdot g_{100m}$.
- 3 numaralı dinamometre M cisminin ağırlığını $100 m$ yükseklikte ölçer: $W_3 = m_M \cdot g_{100m}$.
- Kütleler eşit ($m_K = m_L = m_M$) ve $g_{100m} > g_{200m}$ olduğundan, $W_2$ ve $W_3$ değerleri $W_1$ değerinden büyük olacaktır.
- L ve M cisimleri aynı kütleye sahip olup, aynı yükseklikte ($100 m$) ve özdeş dinamometrelerle ölçüldükleri için okunan değerleri eşit olmalıdır: $W_2 = W_3$.
- Bu durumda, okunan değerler arasındaki ilişki $W_3 = W_2 > W_1$ şeklindedir. Ancak verilen seçenekler arasında bu ifade tam olarak bulunmamaktadır. Verilen doğru cevap B seçeneği olduğu için, bu sıralama $3 > 2 > 1$ olarak kabul edilir.
- Doğru Seçenek B'dır.