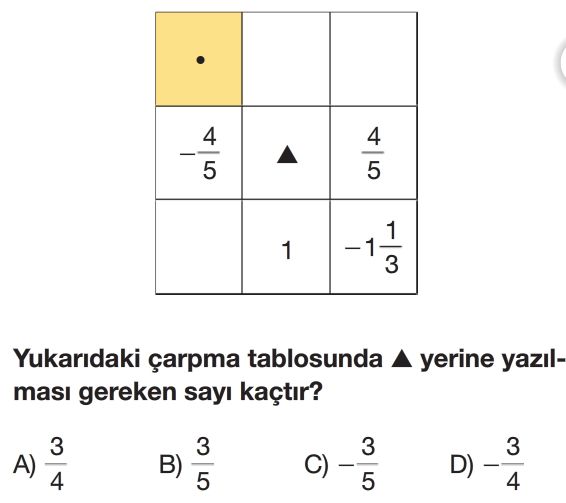
Soru Çözümü
- Karışık kesri bileşik kesre çevirelim.
$-1\frac{1}{3} = -\frac{1 \cdot 3 + 1}{3} = -\frac{4}{3}$ - $\mathbf{\triangle}$ sembolünün değerini bulmak için gerekli ifadeyi belirleyelim.
$\triangle$, ikinci satır başlığı ($R_2$) ile ikinci sütun başlığının ($C_2$) çarpımıdır: $\triangle = R_2 \cdot C_2$ - $C_2$ değerini $R_3$ cinsinden yazalım.
Üçüncü satır başlığı ($R_3$) ile ikinci sütun başlığının ($C_2$) çarpımı $1$'dir: $R_3 \cdot C_2 = 1 \implies C_2 = \frac{1}{R_3}$ - $\triangle$ ifadesini $R_2$ ve $R_3$ oranına dönüştürelim.
$\triangle = R_2 \cdot \frac{1}{R_3} = \frac{R_2}{R_3}$ - $\frac{R_2}{R_3}$ oranını bulalım.
Tablodan $R_2 \cdot C_3 = \frac{4}{5}$ ve $R_3 \cdot C_3 = -\frac{4}{3}$ denklemlerini oranlarsak:
$\frac{R_2 \cdot C_3}{R_3 \cdot C_3} = \frac{\frac{4}{5}}{-\frac{4}{3}} \implies \frac{R_2}{R_3} = \frac{4}{5} \cdot (-\frac{3}{4}) = -\frac{3}{5}$ - Sonucu yerine koyalım.
$\triangle = -\frac{3}{5}$ - Doğru Seçenek C'dır.