Soru Çözümü
- Yeşil kartonların yerleşimini inceleyelim:
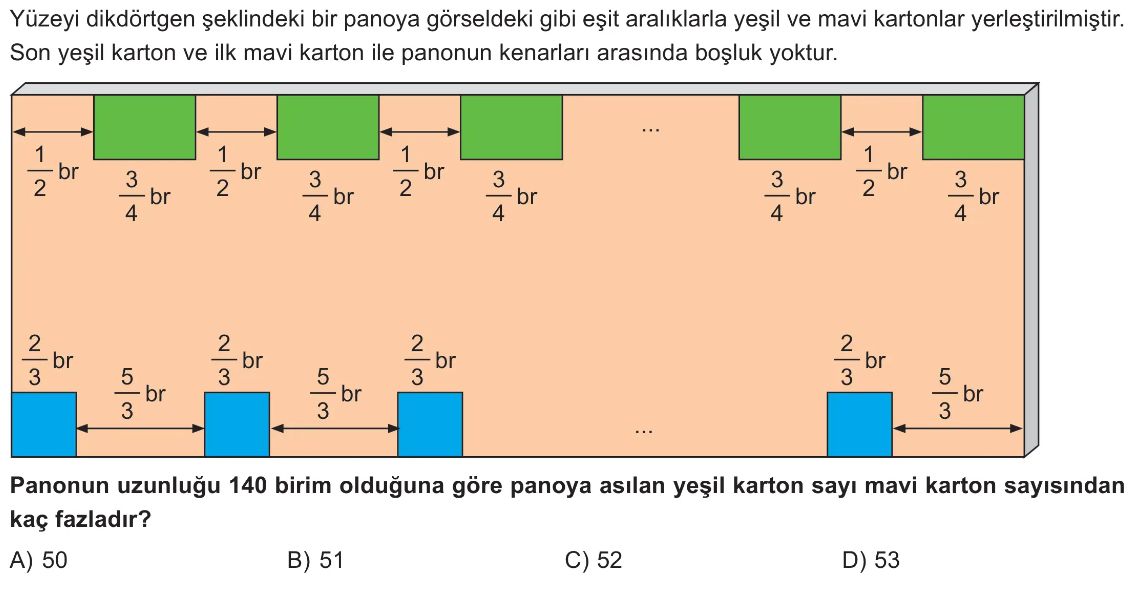
- Bir yeşil kartonun genişliği $3/4$ birimdir.
- Kartonlar arasındaki boşluk $1/2$ birimdir.
- Panonun sol kenarı ile ilk yeşil karton arasında $1/2$ birim boşluk vardır (görselden).
- Sorudaki ifadeye göre, son yeşil karton ile panonun sağ kenarı arasında boşluk yoktur.
- Bu durumda, $N_G$ yeşil karton için toplam uzunluk: $L_G = 1/2 + N_G \times (3/4) + (N_G-1) \times (1/2)$
- $L_G = \frac{1}{2} + \frac{3N_G}{4} + \frac{2N_G-2}{4} = \frac{2 + 3N_G + 2N_G - 2}{4} = \frac{5N_G}{4}$
- Yeşil karton sayısını ($N_G$) bulalım:
- Panonun toplam uzunluğu $140$ birim olduğundan, $\frac{5N_G}{4} = 140$
- $5N_G = 140 \times 4 = 560$
- $N_G = \frac{560}{5} = 112$
- Mavi kartonların yerleşimini inceleyelim:
- Bir mavi kartonun genişliği $2/3$ birimdir.
- Kartonlar arasındaki boşluk $5/3$ birimdir.
- Sorudaki ifadeye göre, panonun sol kenarı ile ilk mavi karton arasında boşluk yoktur.
- Son mavi karton ile panonun sağ kenarı arasında $5/3$ birim boşluk vardır (görselden).
- Bu durumda, $N_B$ mavi karton için toplam uzunluk: $L_B = N_B \times (2/3) + (N_B-1) \times (5/3) + 5/3$
- $L_B = \frac{2N_B}{3} + \frac{5N_B-5}{3} + \frac{5}{3} = \frac{2N_B + 5N_B - 5 + 5}{3} = \frac{7N_B}{3}$
- Mavi karton sayısını ($N_B$) bulalım:
- Panonun toplam uzunluğu $140$ birim olduğundan, $\frac{7N_B}{3} = 140$
- $7N_B = 140 \times 3 = 420$
- $N_B = \frac{420}{7} = 60$
- Yeşil karton sayısının mavi karton sayısından kaç fazla olduğunu bulalım:
- Fark = $N_G - N_B = 112 - 60 = 52$
- Doğru Seçenek C'dır.