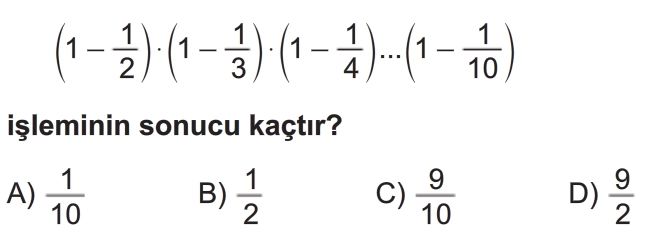
Soru Çözümü
- Öncelikle, her bir parantez içindeki çıkarma işlemlerini yapalım:
- $(1 - \frac{1}{2}) = \frac{2}{2} - \frac{1}{2} = \frac{1}{2}$
- $(1 - \frac{1}{3}) = \frac{3}{3} - \frac{1}{3} = \frac{2}{3}$
- $(1 - \frac{1}{4}) = \frac{4}{4} - \frac{1}{4} = \frac{3}{4}$
- Bu şekilde devam ederek son terimi de bulalım: $(1 - \frac{1}{10}) = \frac{10}{10} - \frac{1}{10} = \frac{9}{10}$
- Şimdi bu terimleri birbiriyle çarpalım: $\frac{1}{2} \cdot \frac{2}{3} \cdot \frac{3}{4} \cdot \dots \cdot \frac{9}{10}$
- Bu çarpımda, her kesrin payı, kendinden sonraki kesrin paydasıyla sadeleşir. Örneğin, ilk kesrin paydası olan $2$, ikinci kesrin payı olan $2$ ile sadeleşir. İkinci kesrin paydası olan $3$, üçüncü kesrin payı olan $3$ ile sadeleşir.
- Bu sadeleşmeler zincirleme şekilde devam eder. Sonuç olarak, sadece ilk kesrin payı ($1$) ve son kesrin paydası ($10$) kalır.
- İşlemin sonucu $\frac{1}{10}$ olur.
- Doğru Seçenek A'dır.