Soru Çözümü
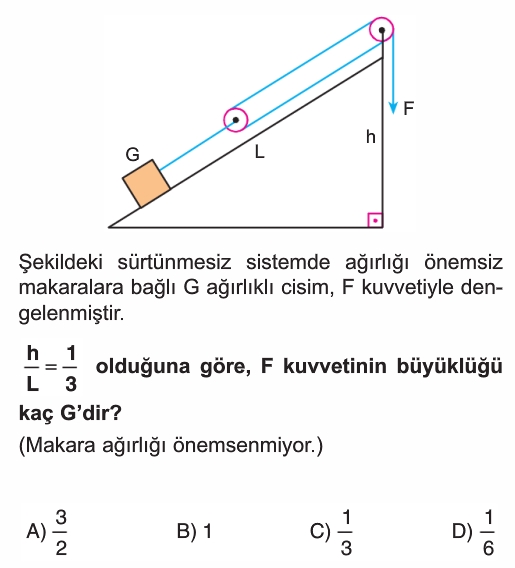
- Eğik düzlemdeki G ağırlığının eğik düzlem boyunca olan bileşeni $G \sin\alpha$'dır.
- Şekildeki dik üçgenden $\sin\alpha = \frac{h}{L}$ olarak bulunur.
- Bu durumda, G ağırlığını eğik düzlemde dengelemek için gereken kuvvet $G \frac{h}{L}$'dir.
- Sistemde bir hareketli makara bulunmaktadır. Hareketli makara, uygulanan kuvveti iki katına çıkarır.
- İpteki gerilme kuvveti F olduğuna göre, hareketli makara G ağırlıklı cisme $2F$ kuvveti uygular.
- Sistem dengede olduğuna göre, $2F = G \frac{h}{L}$ eşitliği sağlanır.
- Soruda $\frac{h}{L} = \frac{1}{3}$ olarak verilmiştir. Bu değeri yerine yazalım: $2F = G \frac{1}{3}$.
- F kuvvetinin büyüklüğünü bulmak için denklemi çözelim: $F = \frac{G}{3 \cdot 2} = \frac{G}{6}$.
- Doğru Seçenek D'dır.