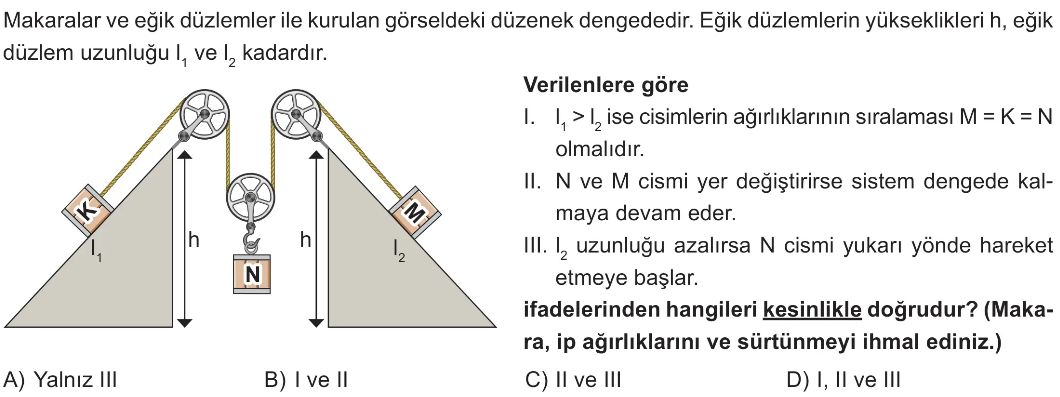
Soru Çözümü
- Sistem dengede olduğundan, her bir cisim ve makara sistemi için kuvvet dengesi yazılır.
- K cismi için eğik düzlemde denge: İpteki gerilme kuvveti $T = K \frac{h}{l_1}$ olur.
- M cismi için eğik düzlemde denge: İpteki gerilme kuvveti $T = M \frac{h}{l_2}$ olur.
- N cismi ve hareketli makara için denge: N cismini yukarı çeken kuvvet $2T$ olduğundan, $N = 2T$ olur.
- Bu denklemlerden $K \frac{h}{l_1} = M \frac{h}{l_2}$ ve $N = 2 K \frac{h}{l_1} = 2 M \frac{h}{l_2}$ bağıntıları elde edilir.
- I. ifadeyi değerlendirelim: Eğer $l_1 > l_2$ ise, $K \frac{h}{l_1} = M \frac{h}{l_2}$ denkleminden $K l_2 = M l_1$ ve dolayısıyla $K = M \frac{l_1}{l_2}$ olur. $l_1 > l_2$ olduğundan $K > M$ olmalıdır. Bu durumda $M=K=N$ sıralaması yanlıştır.
- II. ifadeyi değerlendirelim: N ve M cismi yer değiştirirse, asılı cisim M, sağ eğik düzlemdeki cisim N olur. Yeni denge için $M = 2T'$ ve $T' = N \frac{h}{l_2}$ olmalıdır. Buradan $M = 2 N \frac{h}{l_2}$ elde edilir. Orijinal durumda $N = 2 M \frac{h}{l_2}$ idi. Bu iki denklemin aynı anda sağlanması için $N=M$ ve $l_2 = 2h$ gibi özel koşullar gerekir. Bu koşullar her zaman sağlanmadığı için ifade kesinlikle doğru değildir.
- III. ifadeyi değerlendirelim: Başlangıçta sistem dengededir ve ip gerilimi $T = M \frac{h}{l_2}$ ile belirlenir. N cismini yukarı çeken kuvvet $2T$ kadardır. Eğer $l_2$ uzunluğu azalırsa, $M \frac{h}{l_2}$ değeri artar. Bu durum, M cismini dengede tutmak için gereken ip gerilimi $T$'nin artması anlamına gelir. İp gerilimi $T$ arttığında, N cismini yukarı çeken kuvvet ($2T$) de artar ve N cisminin ağırlığından ($N$) daha büyük hale gelir. Bu nedenle N cismi yukarı yönde hareket etmeye başlar. Bu ifade kesinlikle doğrudur.
- Doğru Seçenek A'dır.