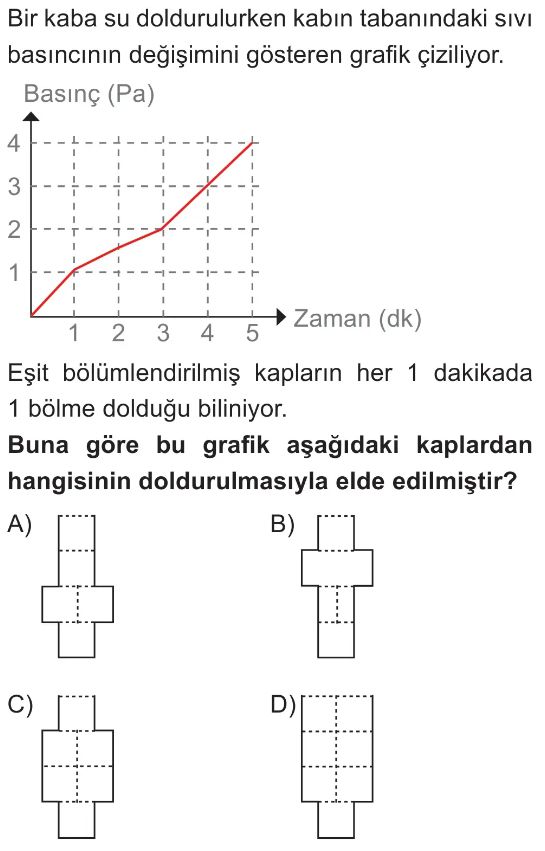
Soru Çözümü
- Sıvı basıncı ($P$), sıvı yüksekliği ($h$) ile doğru orantılıdır ($P = h \cdot d \cdot g$). Bu nedenle, basınç-zaman grafiğinin eğimi, sıvı seviyesinin artış hızı hakkında bilgi verir.
- Grafiğin eğimi ne kadar dikse, sıvı yüksekliği o kadar hızlı artar, bu da kabın o kısmının daha dar olduğunu gösterir. Eğim ne kadar yatıksa, sıvı yüksekliği o kadar yavaş artar, bu da kabın o kısmının daha geniş olduğunu gösterir.
- Grafiği inceleyelim:
- $0-1$ dk aralığı: Basınç $0$'dan $1$ Pa'ya yükselir ($1$ Pa artış). $1$ dakikada $1$ bölme dolar. Bu, kabın ilk kısmının belirli bir genişlikte olduğunu gösterir.
- $1-3$ dk aralığı: Basınç $1$'den $2$ Pa'ya yükselir ($1$ Pa artış). Bu artış $2$ dakika sürer, yani $2$ bölme dolar. Aynı basınç artışı için iki katı süre (ve hacim) gerektiğinden, bu kısmın kesit alanı ilk kısmın iki katı genişliğindedir.
- $3-5$ dk aralığı: Basınç $2$'den $4$ Pa'ya yükselir ($2$ Pa artış). Bu artış $2$ dakika sürer, yani $2$ bölme dolar. $2$ bölme hacimle $2$ Pa basınç artışı sağlandığından, bu kısmın kesit alanı ilk kısımla aynı genişliktedir.
- A seçeneğindeki kabı inceleyelim:
- En alt kısım: $1$ birim yüksekliğinde ve $1$ birim genişliğindedir. $1$ dakikada dolar ve basınç $1$ Pa artar. (Grafiğin $0-1$ dk kısmına uyar)
- Orta kısım: $1$ birim yüksekliğinde ve $2$ birim genişliğindedir. $1$ birim yükseklik için $2$ birim hacim gerektiğinden, $2$ dakikada dolar ve basınç $1$ Pa artar. (Grafiğin $1-3$ dk kısmına uyar)
- En üst kısım: $2$ birim yüksekliğinde ve $1$ birim genişliğindedir. $2$ birim yükseklik için $2$ birim hacim gerektiğinden, $2$ dakikada dolar ve basınç $2$ Pa artar. (Grafiğin $3-5$ dk kısmına uyar)
- A seçeneğindeki kabın dolum süreci, verilen basınç-zaman grafiği ile tamamen uyumludur.
- Doğru Seçenek A'dır.