Soru Çözümü
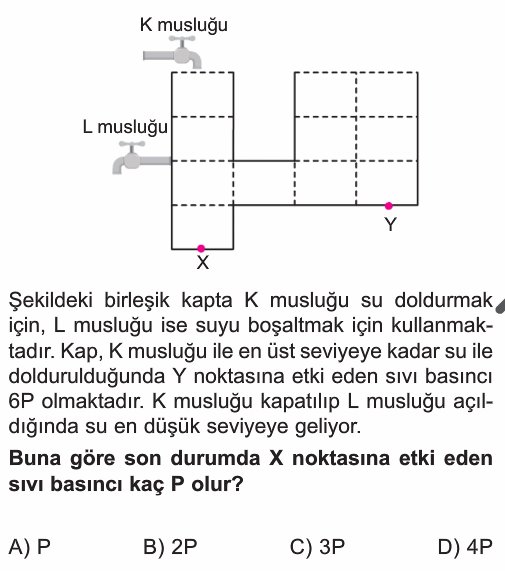
- Her bir kare birim yüksekliğini $h$ olarak kabul edelim. Sıvı basıncı formülü `$P = h \cdot d \cdot g$`'dir.
- Başlangıç Durumu: Kap, K musluğu ile en üst seviyeye kadar doldurulduğunda, suyun taşmadan ulaşabileceği en yüksek seviye sağ kolun yüksekliği olan $3h$'dir. Bu durumda su seviyesi $3h$ olur.
- Y noktasının derinliği $3h$'dir. Y noktasındaki basınç $P_Y = 3hdg = 6P$ olarak verilmiştir.
- Bu bilgiden $hdg = \frac{6P}{3} = 2P$ bağıntısını elde ederiz.
- Son Durum: K musluğu kapatılıp L musluğu açıldığında, su seviyesi L musluğunun seviyesine kadar düşer. L musluğu yerden $2h$ yükseklikte olduğundan, son su seviyesi $2h$ olur.
- X noktasının derinliği $2h$'dir. X noktasındaki basınç $P_X = 2hdg$ olur.
- $hdg = 2P$ değerini $P_X$ denkleminde yerine koyarsak, $P_X = 2 \cdot (2P) = 4P$ bulunur.
- Doğru Seçenek D'dır.