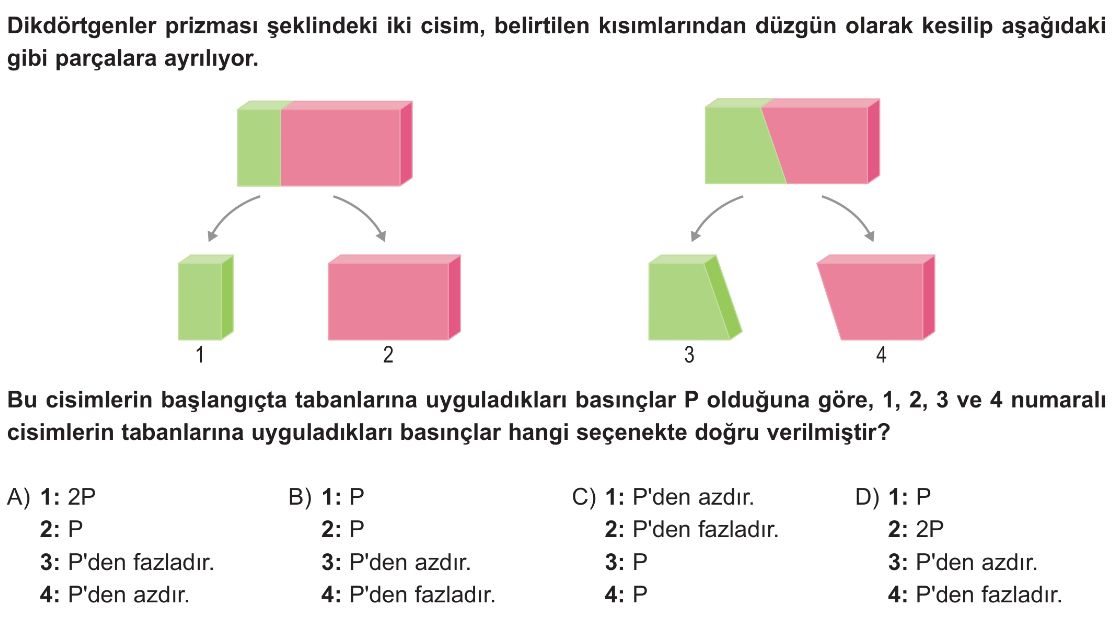
Soru Çözümü
- Katı cisimlerde basınç, cismin ağırlığının taban alanına oranıdır: $P = \frac{G}{A}$. Düzgün geometrili cisimler için $P = \rho \cdot h \cdot g$ formülü de kullanılabilir. Başlangıçtaki cisimlerin basıncı $P$ olduğuna göre, yoğunlukları $\rho$ ve yükseklikleri $h$ aynıdır.
- 1 numaralı cisim: Başlangıçtaki yeşil prizmanın dikey olarak kesilmesiyle oluşan, daha küçük bir dikdörtgenler prizmasıdır. Yüksekliği ve yoğunluğu değişmediği için basıncı başlangıçtaki basınç $P$ ile aynıdır. Yani $P_1 = P$.
- 2 numaralı cisim: Başlangıçtaki pembe prizmanın dikey olarak kesilmesiyle oluşan, daha küçük bir dikdörtgenler prizmasıdır. Yüksekliği ve yoğunluğu değişmediği için basıncı başlangıçtaki basınç $P$ ile aynıdır. Yani $P_2 = P$.
- 3 numaralı cisim: Başlangıçtaki yeşil prizmanın çapraz olarak kesilmesiyle oluşan bir yamuk prizmadır. Taban alanı başlangıçtaki yeşil prizmanın taban alanı ile aynıdır ($A_3 = A_{başlangıç}$). Ancak, cismin bir kısmı kesilip alındığı için ağırlığı başlangıçtaki yeşil prizmanın ağırlığından daha azdır ($G_3 < G_{başlangıç}$). Dolayısıyla basıncı P'den azdır. Yani $P_3 < P$.
- 4 numaralı cisim: Başlangıçtaki pembe prizmanın çapraz olarak kesilmesiyle oluşan bir yamuk prizmadır. Taban alanı başlangıçtaki pembe prizmanın taban alanı ile aynıdır ($A_4 = A_{başlangıç}$). Ancak, çapraz kesimden dolayı cismin hacmi (ve dolayısıyla ağırlığı) başlangıçtaki pembe prizmanın ağırlığından daha fazladır ($G_4 > G_{başlangıç}$). Dolayısıyla basıncı P'den fazladır. Yani $P_4 > P$.
- Bu sonuçlara göre, doğru seçenek B'dir.