Soru Çözümü
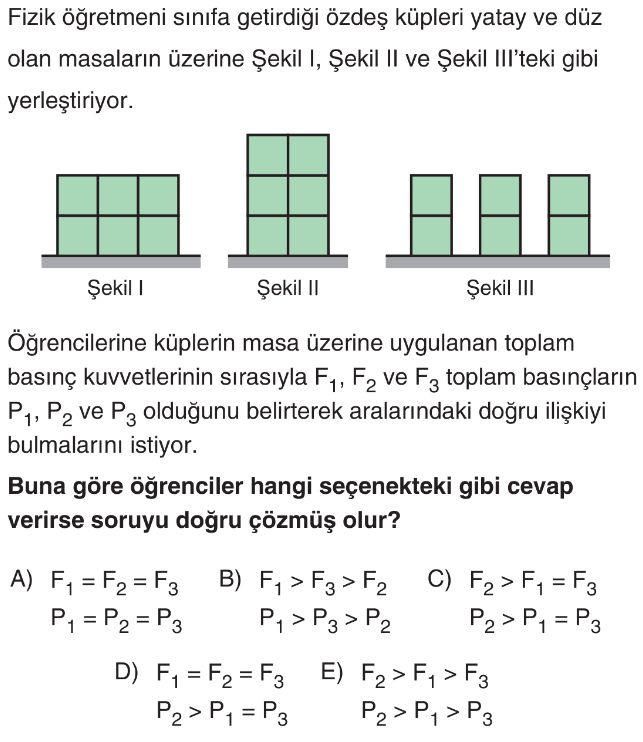
- Her bir şekildeki toplam küp sayısı 6'dır.
- Özdeş küplerin her birinin ağırlığı $G$ olsun. Masa üzerine uygulanan toplam basınç kuvveti, küplerin toplam ağırlığına eşittir.
- Bu durumda, $F_1 = 6G$, $F_2 = 6G$, $F_3 = 6G$. Dolayısıyla, $F_1 = F_2 = F_3$.
- Basınç ($P$), kuvvetin yüzeye temas eden alana oranıdır ($P = \frac{F}{A}$). Her bir küpün taban alanı $A$ olsun.
- Şekil I'de 6 küp vardır ve 3 küp yüzeye temas etmektedir. Temas alanı $A_1 = 3A$. Basınç $P_1 = \frac{6G}{3A} = \frac{2G}{A}$.
- Şekil II'de 6 küp vardır ve 2 küp yüzeye temas etmektedir. Temas alanı $A_2 = 2A$. Basınç $P_2 = \frac{6G}{2A} = \frac{3G}{A}$.
- Şekil III'te 6 küp vardır ve 3 küp yüzeye temas etmektedir (her bir yığının altındaki 1 küp). Temas alanı $A_3 = 3A$. Basınç $P_3 = \frac{6G}{3A} = \frac{2G}{A}$.
- Basınçları karşılaştırırsak: $P_2 = \frac{3G}{A}$, $P_1 = \frac{2G}{A}$, $P_3 = \frac{2G}{A}$. Buradan $P_2 > P_1 = P_3$ ilişkisi elde edilir.
- Doğru Seçenek D'dır.