Soru Çözümü
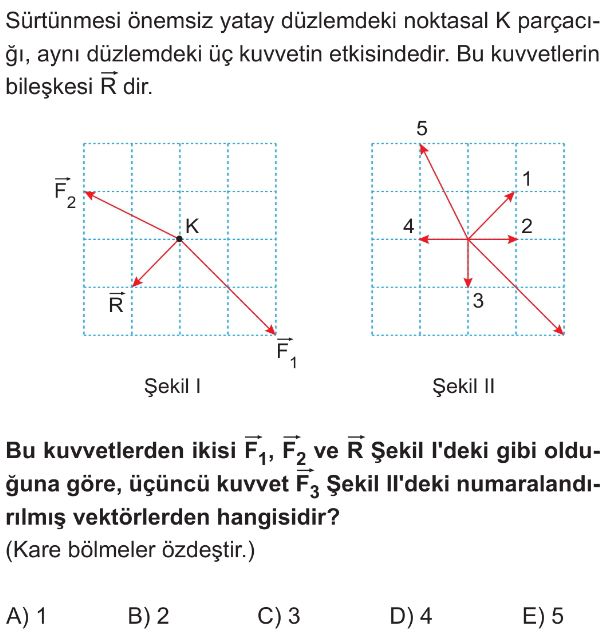
- Şekil I'deki kuvvet vektörlerini bileşenlerine ayıralım (K noktasını orijin kabul ederek):
- $\vec{F_1} = (3, -3)$
- $\vec{F_2} = (-3, 2)$
- $\vec{R} = (-2, -1)$
- Üç kuvvetin bileşkesi $\vec{R}$ olduğundan, $\vec{R} = \vec{F_1} + \vec{F_2} + \vec{F_3}$ denklemini kullanırız.
- $\vec{F_3}$ kuvvetini bulmak için denklemi düzenleyelim: $\vec{F_3} = \vec{R} - \vec{F_1} - \vec{F_2}$.
- Önce $\vec{F_1} + \vec{F_2}$ toplamını bulalım:
- $\vec{F_1} + \vec{F_2} = (3 + (-3), -3 + 2) = (0, -1)$
- Şimdi $\vec{F_3}$ kuvvetini hesaplayalım:
- $\vec{F_3} = (-2, -1) - (0, -1)$
- $\vec{F_3} = (-2 - 0, -1 - (-1))$
- $\vec{F_3} = (-2, 0)$
- Şekil II'deki vektörleri inceleyelim:
- 1 numaralı vektör: $(1, 1)$
- 2 numaralı vektör: $(2, 0)$
- 3 numaralı vektör: $(0, -2)$
- 4 numaralı vektör: $(-2, 0)$
- 5 numaralı vektör: $(0, 2)$
- Hesapladığımız $\vec{F_3} = (-2, 0)$ vektörü, Şekil II'deki 4 numaralı vektöre karşılık gelmektedir.
- Doğru Seçenek D'dır.