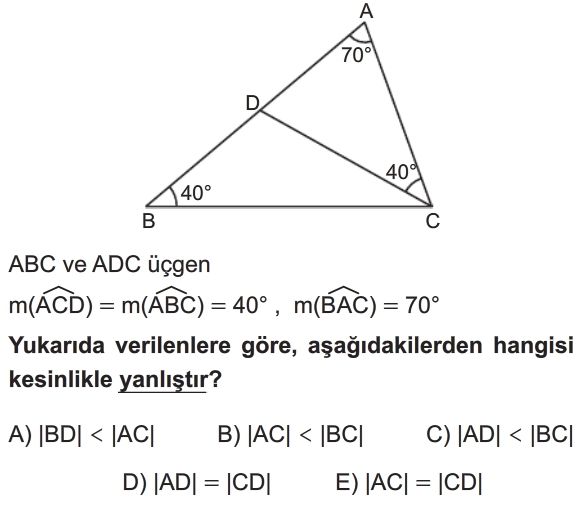
Soru Çözümü
- $\triangle ABC$'de açıları hesaplayalım: $m(\widehat{ABC}) = 40^\circ$, $m(\widehat{BAC}) = 70^\circ$. Üçgenin iç açıları toplamı $180^\circ$ olduğundan, $m(\widehat{ACB}) = 180^\circ - (40^\circ + 70^\circ) = 70^\circ$.
- $m(\widehat{ACD}) = 40^\circ$ verildiği için, $m(\widehat{DCB}) = m(\widehat{ACB}) - m(\widehat{ACD}) = 70^\circ - 40^\circ = 30^\circ$ olur.
- $\triangle BDC$'de $m(\widehat{DBC}) = 40^\circ$ ve $m(\widehat{DCB}) = 30^\circ$. $m(\widehat{ADC})$ açısı $\triangle BDC$'nin dış açısıdır. Bu nedenle $m(\widehat{ADC}) = m(\widehat{DBC}) + m(\widehat{DCB}) = 40^\circ + 30^\circ = 70^\circ$.
- Şimdi $\triangle ADC$'nin açılarını belirleyelim: $m(\widehat{ACD}) = 40^\circ$ ve $m(\widehat{ADC}) = 70^\circ$. Üçgenin iç açıları toplamından $m(\widehat{CAD}) = 180^\circ - (40^\circ + 70^\circ) = 70^\circ$.
- $\triangle ADC$'deki açılar: $m(\widehat{ACD}) = 40^\circ$, $m(\widehat{CAD}) = 70^\circ$, $m(\widehat{ADC}) = 70^\circ$. Bir üçgende büyük açı karşısında büyük kenar bulunur.
- $m(\widehat{CAD}) = m(\widehat{ADC}) = 70^\circ$ olduğundan, bu açıların karşısındaki kenarlar eşit olmalıdır: $|CD| = |AC|$.
- $m(\widehat{ACD}) = 40^\circ$ en küçük açı olduğundan, karşısındaki kenar $|AD|$ en kısa kenardır.
- Bu durumda, $|AD| < |CD|$ ve $|AD| < |AC|$ ilişkisi geçerlidir.
- Seçenek D) $|AD| = |CD|$ ifadesini inceleyelim. Yukarıdaki analizimize göre, $\triangle ADC$'de $40^\circ$ karşısında $|AD|$ ve $70^\circ$ karşısında $|CD|$ kenarı bulunmaktadır. Dolayısıyla $|AD| < |CD|$ olmalıdır. Bu nedenle $|AD| = |CD|$ ifadesi kesinlikle yanlıştır.
- Doğru Seçenek D'dır.