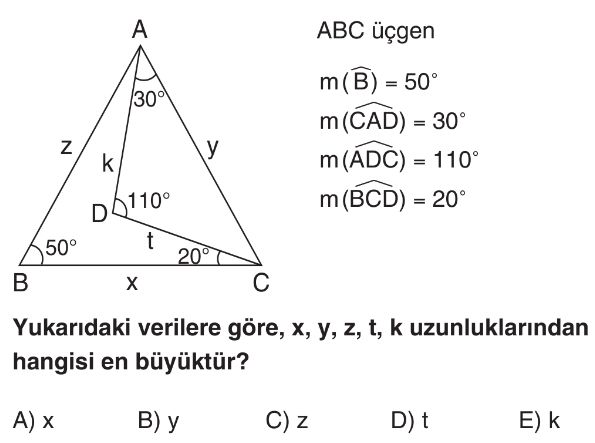
Soru Çözümü
- $\triangle ADC$'deki açılar hesaplanır. $m(\hat{CAD}) = 30^\circ$ ve $m(\hat{ADC}) = 110^\circ$ olduğundan, $m(\hat{ACD}) = 180^\circ - (30^\circ + 110^\circ) = 40^\circ$ bulunur.
- $\triangle ADC$'de açı-kenar ilişkisi uygulanır. $110^\circ > 40^\circ > 30^\circ$ olduğundan, karşılarındaki kenarlar için $y > k > t$ sıralaması geçerlidir.
- $\triangle ABC$'deki açılar hesaplanır. $m(\hat{B}) = 50^\circ$ ve $m(\hat{C}) = m(\hat{ACD}) = 40^\circ$ olduğundan, $m(\hat{BAC}) = 180^\circ - (50^\circ + 40^\circ) = 90^\circ$ bulunur.
- $\triangle ABC$'de açı-kenar ilişkisi uygulanır. $90^\circ > 50^\circ > 40^\circ$ olduğundan, karşılarındaki kenarlar için $x > y > z$ sıralaması geçerlidir.
- $\triangle ABD$'deki açılar hesaplanır. $m(\hat{BAD}) = m(\hat{BAC}) - m(\hat{CAD}) = 90^\circ - 30^\circ = 60^\circ$. $m(\hat{ABD}) = 50^\circ$ olduğundan, $m(\hat{ADB}) = 180^\circ - (60^\circ + 50^\circ) = 70^\circ$ bulunur.
- $\triangle ABD$'de açı-kenar ilişkisi uygulanır. $70^\circ > 50^\circ$ olduğundan, karşılarındaki kenarlar için $z > k$ sıralaması geçerlidir. ($m(\hat{ADB})$ karşısında $z$, $m(\hat{ABD})$ karşısında $k$ vardır.)
- Tüm kenar uzunlukları karşılaştırılır: $x > y > z$ ve $y > k > t$ ve $z > k$. Bu eşitsizlikler birleştirildiğinde $x > y > z > k > t$ elde edilir.
- Buna göre en büyük uzunluk $x$'tir.
- Doğru Seçenek A'dır.