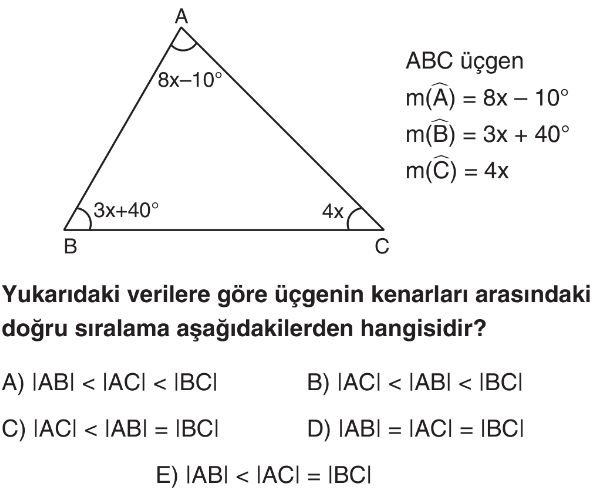
Soru Çözümü
- Bir üçgenin iç açılarının toplamı $180^\circ$'dir. Verilen açıları toplayalım: $(8x - 10^\circ) + (3x + 40^\circ) + 4x = 180^\circ$
- Denklemi çözerek $x$ değerini bulalım: $15x + 30^\circ = 180^\circ$ $15x = 150^\circ$ $x = 10^\circ$
- $x$ değerini yerine koyarak her bir açının ölçüsünü hesaplayalım: $m(\widehat{A}) = 8(10^\circ) - 10^\circ = 80^\circ - 10^\circ = 70^\circ$ $m(\widehat{B}) = 3(10^\circ) + 40^\circ = 30^\circ + 40^\circ = 70^\circ$ $m(\widehat{C}) = 4(10^\circ) = 40^\circ$
- Açıları küçükten büyüğe sıralayalım: $m(\widehat{C}) < m(\widehat{A}) = m(\widehat{B})$ $40^\circ < 70^\circ = 70^\circ$
- Bir üçgende büyük açı karşısında büyük kenar, eşit açılar karşısında eşit kenarlar bulunur. $\widehat{C}$ açısının karşısındaki kenar $|AB|$'dir. $\widehat{A}$ açısının karşısındaki kenar $|BC|$'dir. $\widehat{B}$ açısının karşısındaki kenar $|AC|$'dir.
- Kenarlar arasındaki sıralama açı sıralamasıyla aynı olacaktır: $|AB| < |BC| = |AC|$
- Bu sıralama, seçeneklerdeki $|AB| < |AC| = |BC|$ ifadesiyle aynıdır.
- Doğru Seçenek E'dır.