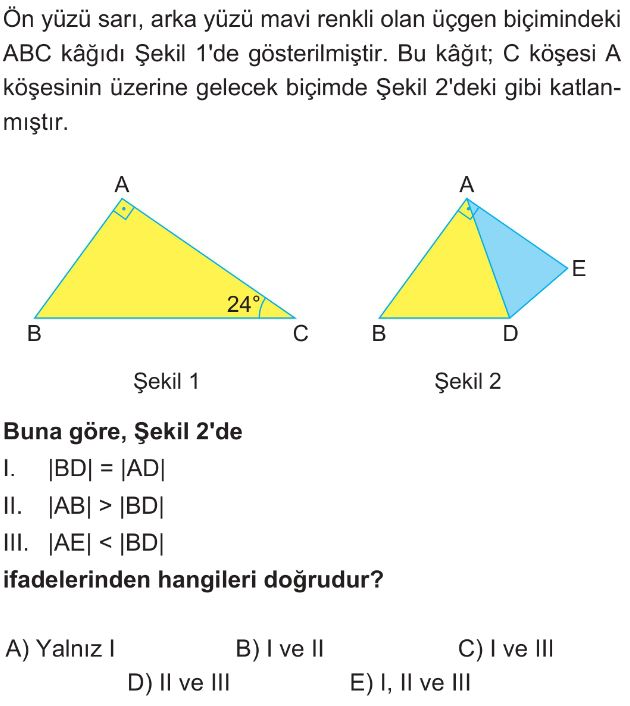
Soru Çözümü
- Şekil 1'deki $\triangle ABC$ dik üçgeninde $\angle A = 90^\circ$ ve $\angle C = 24^\circ$ verilmiştir. Bu durumda $\angle B = 180^\circ - 90^\circ - 24^\circ = 66^\circ$ olur.
- C köşesi A köşesinin üzerine katlandığında, katlama çizgisi AC doğru parçasının dik orta noktasıdır. Bu durumda, katlama çizgisi üzerindeki her nokta A ve C'ye eşit uzaklıktadır. D noktası katlama çizgisi üzerinde olduğundan $|AD| = |CD|$ olur.
- I. ifade: $|BD| = |AD|$
$|AD| = |CD|$ olduğundan, $\triangle ADC$ ikizkenar üçgendir. Bu durumda $\angle DAC = \angle DCA = 24^\circ$ olur.
$\angle BAD = \angle BAC - \angle DAC = 90^\circ - 24^\circ = 66^\circ$ bulunur.
$\triangle ABD$'de $\angle B = 66^\circ$ ve $\angle BAD = 66^\circ$ olduğundan, $\triangle ABD$ ikizkenar üçgendir ve $|AD| = |BD|$'dir.
Dolayısıyla, I. ifade doğrudur. - II. ifade: $|AB| > |BD|$
$\triangle ABD$'de $\angle B = 66^\circ$, $\angle BAD = 66^\circ$ ve $\angle ADB = 180^\circ - 66^\circ - 66^\circ = 48^\circ$'dir.
Bir üçgende büyük açı karşısında büyük kenar bulunur. Bu durumda, $66^\circ > 48^\circ$ olduğundan $|AD| = |BD| > |AB|$ olur.
Dolayısıyla, $|AB| < |BD|$'dir. Verilen ifade yanlıştır.
Dolayısıyla, II. ifade yanlıştır. - III. ifade: $|AE| < |BD|$
C köşesi A üzerine katlandığında, CE kenarı AE kenarı üzerine gelir. Bu yüzden $|AE| = |CE|$'dir.
Ayrıca, katlama sonucunda $\triangle CDE \cong \triangle ADE$ olur. Bu durumda $\angle CDE = \angle ADE$'dir.
$\triangle ADC$'de $\angle DAC = 24^\circ$ ve $\angle DCA = 24^\circ$ olduğundan $\angle ADC = 180^\circ - 24^\circ - 24^\circ = 132^\circ$'dir.
$\angle ADE = \angle ADC / 2 = 132^\circ / 2 = 66^\circ$'dir.
$\triangle ADE$'de $\angle EAD = 24^\circ$ (katlama nedeniyle $\angle C$'ye eşittir) ve $\angle ADE = 66^\circ$'dir.
$\angle AED = 180^\circ - 24^\circ - 66^\circ = 90^\circ$'dir. Yani $\triangle ADE$ bir dik üçgendir.
$\triangle ADE$'de $\sin(\angle EAD) = |AE| / |AD|$'dir. Yani $\sin(24^\circ) = |AE| / |AD|$'dir.
Buradan $|AE| = |AD| \sin(24^\circ)$ elde edilir. $\sin(24^\circ) < 1$ olduğundan $|AE| < |AD|$'dir.
I. ifadeden $|AD| = |BD|$ olduğunu biliyoruz. Bu durumda $|AE| < |BD|$ olur.
Dolayısıyla, III. ifade doğrudur. - Doğru Seçenek C'dır.