Soru Çözümü
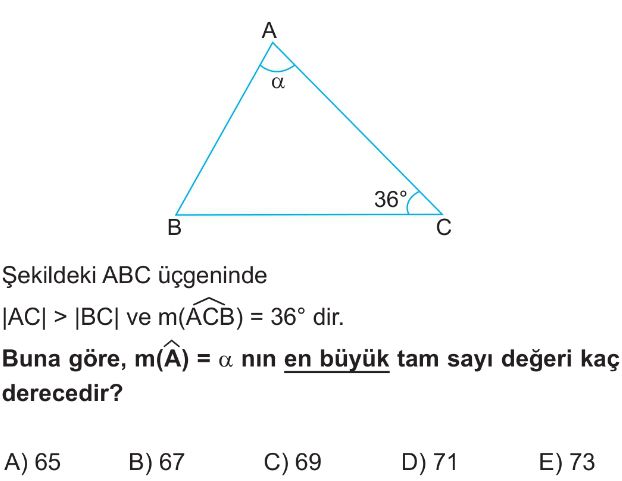
- Bir üçgende, büyük kenarın karşısında büyük açı bulunur. Verilen bilgiye göre $|AC| > |BC|$ olduğundan, $AC$ kenarının karşısındaki açı olan $m(\widehat{B})$ açısı, $BC$ kenarının karşısındaki açı olan $m(\widehat{A}) = \alpha$ açısından daha büyüktür. Yani, $m(\widehat{B}) > \alpha$.
- Üçgenin iç açıları toplamı $180^\circ$'dir. Bu durumda $m(\widehat{A}) + m(\widehat{B}) + m(\widehat{C}) = 180^\circ$ olur.
- Verilen açı değerlerini yerine koyarsak: $\alpha + m(\widehat{B}) + 36^\circ = 180^\circ$. Buradan $m(\widehat{B}) = 180^\circ - 36^\circ - \alpha = 144^\circ - \alpha$ bulunur.
- İlk adımda bulduğumuz $m(\widehat{B}) > \alpha$ eşitsizliğinde $m(\widehat{B})$ yerine $144^\circ - \alpha$ yazalım: $144^\circ - \alpha > \alpha$.
- Bu eşitsizliği çözersek: $144^\circ > 2\alpha \Rightarrow \alpha < 72^\circ$.
- $\alpha$ bir üçgenin açısı olduğu için pozitif olmalıdır ($ \alpha > 0 $). Ayrıca $m(\widehat{B}) = 144^\circ - \alpha > 0$ olduğundan $\alpha < 144^\circ$ olmalıdır. $\alpha < 72^\circ$ koşulu bu iki durumu da sağlar.
- $\alpha < 72^\circ$ eşitsizliğine göre, $\alpha$'nın alabileceği en büyük tam sayı değeri $71^\circ$'dir.
- Doğru Seçenek D'dır.