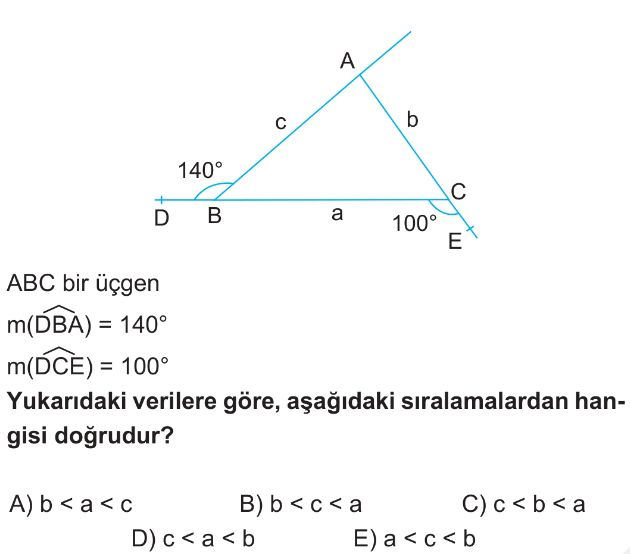
Soru Çözümü
- $m(\widehat{ABC})$ açısı, $m(\widehat{DBA})$ açısının bütünleridir. Bu nedenle $m(\widehat{ABC}) = 180^\circ - 140^\circ = 40^\circ$
- $m(\widehat{BCA})$ açısı, $m(\widehat{DCE})$ açısının bütünleridir. Bu nedenle $m(\widehat{BCA}) = 180^\circ - 100^\circ = 80^\circ$
- Üçgenin iç açıları toplamı $180^\circ$ olduğundan, $m(\widehat{BAC}) = 180^\circ - (40^\circ + 80^\circ) = 180^\circ - 120^\circ = 60^\circ$
- Üçgenin açıları $m(\widehat{B}) = 40^\circ$, $m(\widehat{A}) = 60^\circ$ ve $m(\widehat{C}) = 80^\circ$ olarak bulunur.
- Açıların büyüklük sıralaması $m(\widehat{B}) < m(\widehat{A}) < m(\widehat{C})$ şeklindedir.
- Bir üçgende büyük açı karşısında büyük kenar, küçük açı karşısında küçük kenar bulunur.
- Bu durumda kenar uzunlukları sıralaması $b < a < c$ olur.
- Doğru Seçenek A'dır.