Soru Çözümü
- Üçgenin iç açıları toplamı $180^\circ$'dir.
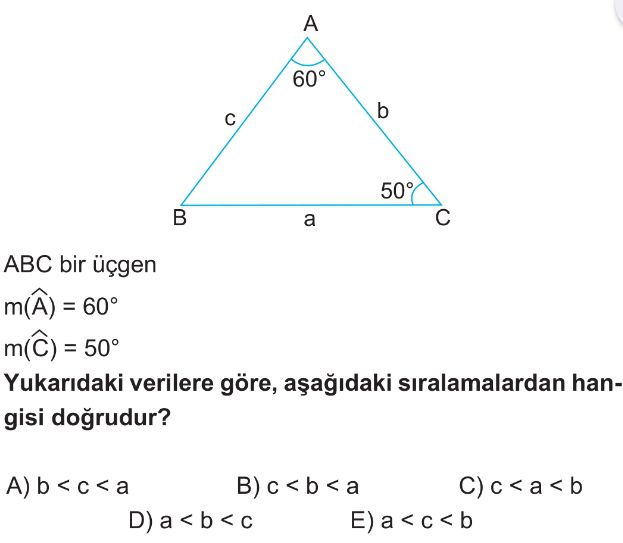
- Verilen açılar: $m(\hat{A}) = 60^\circ$ ve $m(\hat{C}) = 50^\circ$.
- $m(\hat{B})$ açısını bulalım: $m(\hat{B}) = 180^\circ - (60^\circ + 50^\circ) = 180^\circ - 110^\circ = 70^\circ$.
- Açıları küçükten büyüğe sıralayalım: $m(\hat{C}) < m(\hat{A}) < m(\hat{B})$. Yani $50^\circ < 60^\circ < 70^\circ$.
- Bir üçgende büyük açı karşısında büyük kenar, küçük açı karşısında küçük kenar bulunur.
- Bu durumda kenar uzunlukları sıralaması: c < a < b.
- Doğru Seçenek C'dır.