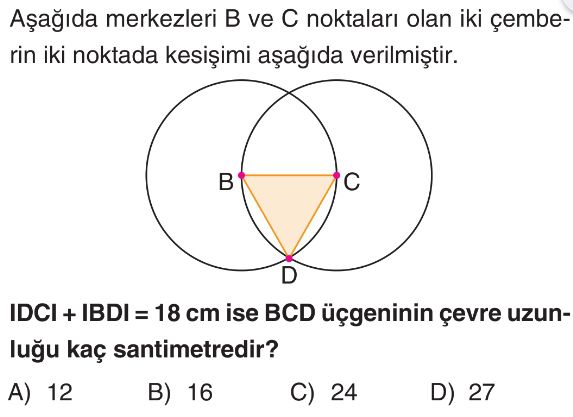
Soru Çözümü
- Bir çemberin merkezi ile üzerindeki herhangi bir nokta arasındaki uzaklık (yarıçap) her zaman aynıdır.
- B merkezli çemberde, D ve C noktaları çemberin üzerindedir. Bu nedenle, $|BD|$ uzunluğu ile $|BC|$ uzunluğu birbirine eşittir: $|BD| = |BC|$.
- C merkezli çemberde, D ve B noktaları çemberin üzerindedir. Bu nedenle, $|CD|$ uzunluğu ile $|CB|$ uzunluğu birbirine eşittir: $|CD| = |CB|$.
- Yukarıdaki iki eşitlikten, BCD üçgeninin tüm kenar uzunlukları birbirine eşittir: $|BD| = |CD| = |BC|$. Bu, BCD üçgeninin bir eşkenar üçgen olduğunu gösterir.
- Soruda verilen bilgiye göre, $|DC| + |BD| = 18 cm$.
- $|DC|$ ve $|BD|$ birbirine eşit olduğu için, bu ifadeyi `$|BD| + |BD| = 18 cm$` şeklinde yazabiliriz.
- Bu durumda, `$2 \times |BD| = 18 cm$` olur.
- Her iki tarafı $2$'ye bölersek, `$|BD| = 18 \div 2 = 9 cm$` bulunur.
- BCD üçgeninin çevresi, üç kenarının uzunlukları toplamıdır: $|BD| + |CD| + |BC|$.
- Her kenar $9 cm$ olduğu için, üçgenin çevresi `$9 cm + 9 cm + 9 cm = 27 cm$` olur.
- Doğru Seçenek D'dır.