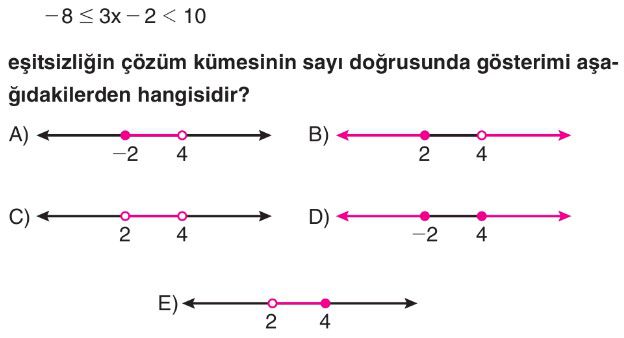
Soru Çözümü
- Verilen eşitsizlik: $-8 \leq 3x - 2 < 10$
- Eşitsizliğin her tarafına $2$ ekleyelim: $-8 + 2 \leq 3x - 2 + 2 < 10 + 2$
- Bu işlem sonucunda eşitsizlik: $-6 \leq 3x < 12$ olur
- Eşitsizliğin her tarafını $3$'e bölelim: $\frac{-6}{3} \leq \frac{3x}{3} < \frac{12}{3}$
- Bu işlem sonucunda eşitsizlik: $-2 \leq x < 4$ olarak bulunur
- Bu çözüm kümesi, sayı doğrusunda $-2$ dahil (kapalı nokta) ve $4$ hariç (açık nokta) aralığı temsil eder.
- Bu gösterim A seçeneğinde doğru şekilde verilmiştir.
- Doğru Seçenek A'dır.