Soru Çözümü
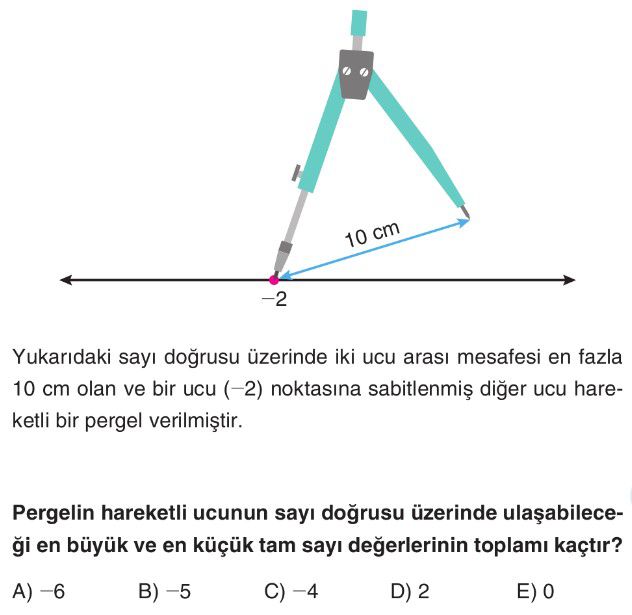
- Sabit uç $F = -2$ noktasındadır. Hareketli uç $M$ olsun. İki uç arasındaki mesafe en fazla $10$ cm'dir.
- Bu durumu mutlak değer eşitsizliği ile ifade ederiz: $|M - (-2)| \le 10$.
- Eşitsizliği düzenlersek: $|M + 2| \le 10$.
- Mutlak değer eşitsizliğini açarsak: $-10 \le M + 2 \le 10$.
- Her taraftan $2$ çıkararak $M$ değer aralığını buluruz: $-10 - 2 \le M \le 10 - 2 \implies -12 \le M \le 8$.
- Hareketli ucun ulaşabileceği en büyük tam sayı değeri $M_{maks} = 8$'dir.
- Hareketli ucun ulaşabileceği en küçük tam sayı değeri $M_{min} = -12$'dir.
- Bu iki değerin toplamı $8 + (-12) = 8 - 12 = -4$'tür.
- Doğru Seçenek C'dır.