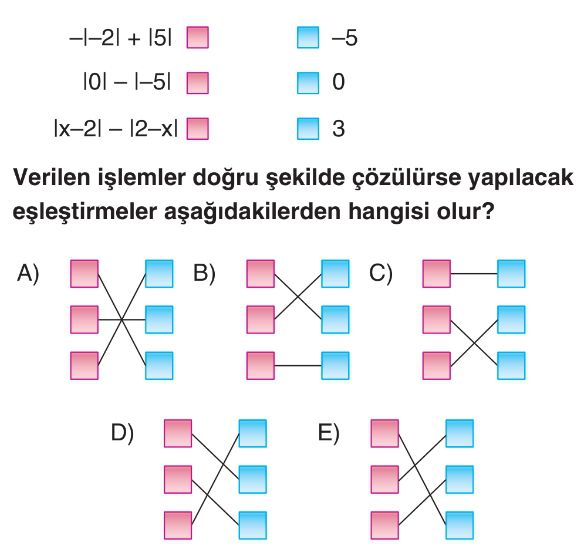
Soru Çözümü
- İlk ifadeyi hesaplayın:
`$-|-2| + |5|$`
Mutlak değerleri hesaplayın: `$|-2| = 2$` ve `$|5| = 5$`.
İfadeyi yerine koyun: `$-(2) + 5 = -2 + 5 = 3$`
Bu ifade `$3$` ile eşleşir. - İkinci ifadeyi hesaplayın:
`$-|0| - |-5|$`
Mutlak değerleri hesaplayın: `$|0| = 0$` ve `$|-5| = 5$`.
İfadeyi yerine koyun: `$-(0) - 5 = 0 - 5 = -5$`
Bu ifade `$-5$` ile eşleşir. - Üçüncü ifadeyi hesaplayın:
`$-|x-2| - |2-x|$`
Mutlak değer özelliğinden `$|a-b| = |b-a|$` olduğu için `$|x-2| = |2-x|$`.
İfadeyi yeniden yazın: `$-|x-2| - |x-2| = -2|x-2|$`
Kalan sonuç `$0$`'dır. Bu ifadenin `$0$` olması için `$|x-2|=0$` yani `$x=2$` olması gerekir. Diğer sonuçlar `$3$` (mutlak değer negatif olamayacağından imkansız) ve `$-5$` (bu durumda `$|x-2| = 5/2$`) idi. Problem bir eşleştirme sorusu olduğundan, bu ifadenin kalan sonuç olan `$0$` ile eşleştiğini kabul ederiz.
Bu ifade `$0$` ile eşleşir. - Eşleştirmeleri özetleyin:
- `$-|-2| + |5| \rightarrow 3$`
- `$-|0| - |-5| \rightarrow -5$`
- `$-|x-2| - |2-x| \rightarrow 0$`
- Doğru Seçenek E'dır.