Soru Çözümü
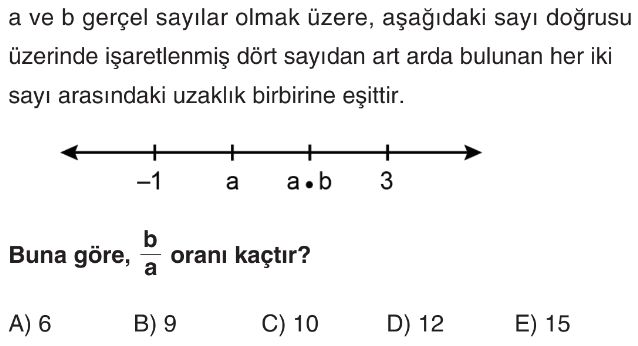
- Sayı doğrusundaki dört sayı $-1$, $a$, $a \cdot b$, $3$'tür. Ardışık sayılar arasındaki mesafe eşittir.
- $-1$ ile $3$ arasındaki toplam mesafe $3 - (-1) = 4$'tür. Bu mesafe $3$ eşit aralığa bölünmüştür.
- Her bir aralığın mesafesi ($d$) $d = \frac{4}{3}$ olarak bulunur.
- İlk aralığı kullanarak $a$ değerini bulalım: $a = -1 + d = -1 + \frac{4}{3} = \frac{-3+4}{3} = \frac{1}{3}$.
- İkinci aralığı kullanarak $a \cdot b$ değerini bulalım: $a \cdot b = a + d = \frac{1}{3} + \frac{4}{3} = \frac{5}{3}$.
- $a \cdot b = \frac{5}{3}$ ve $a = \frac{1}{3}$ olduğuna göre, $b$ değerini bulalım: $(\frac{1}{3}) \cdot b = \frac{5}{3} \Rightarrow b = 5$.
- Son olarak, $\frac{b}{a}$ oranını hesaplayalım: $\frac{b}{a} = \frac{5}{\frac{1}{3}} = 5 \cdot 3 = 15$.
- Doğru Seçenek E'dır.