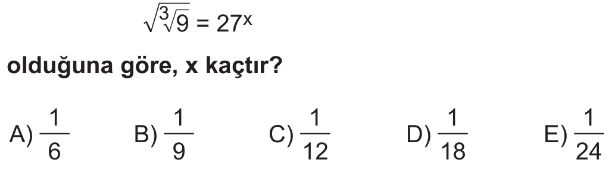
Soru Çözümü
- Verilen denklemi yazalım: `$\sqrt[3]{\sqrt{9}} = 27^x$`
- Öncelikle iç kökü hesaplayalım: `$\sqrt{9} = 3$`
- Denklem şimdi `$\sqrt[3]{3} = 27^x$` haline gelir.
- Sol tarafı üslü ifade olarak yazalım: `$\sqrt[3]{3} = 3^{\frac{1}{3}}$`
- Sağ tarafı `$3$` tabanında yazalım: `$27 = 3^3$`. Bu durumda `$27^x = (3^3)^x = 3^{3x}$` olur.
- Denklemi yeniden düzenleyelim: `$3^{\frac{1}{3}} = 3^{3x}$`
- Tabanlar eşit olduğundan, üsler de eşit olmalıdır: `$\frac{1}{3} = 3x$`
- `$x$` değerini bulmak için her iki tarafı `$3$`'e bölelim: `$x = \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{9}$`
- Doğru Seçenek B'dır.