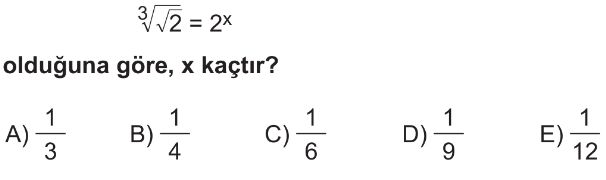
Soru Çözümü
- Verilen denklem `$\sqrt[3]{\sqrt{2}} = 2^x$` şeklindedir.
- Öncelikle içteki köklü ifadeyi üslü sayı olarak yazalım: `$\sqrt{2} = 2^{1/2}$`.
- Şimdi bu ifadeyi dıştaki küp kökün içine yerleştirelim: `$\sqrt[3]{2^{1/2}}$`.
- Küpkökü de üslü sayı olarak yazarsak `$(2^{1/2})^{1/3}$` elde ederiz.
- Üslü sayılarda üslerin çarpımı kuralını uygulayalım: `$2^{(1/2) \cdot (1/3)} = 2^{1/6}$`.
- Denklemimiz artık `$2^{1/6} = 2^x$` şeklindedir.
- Tabanlar eşit olduğundan, üsler de eşit olmalıdır: `$x = 1/6$`.
- Doğru Seçenek C'dır.