Soru Çözümü
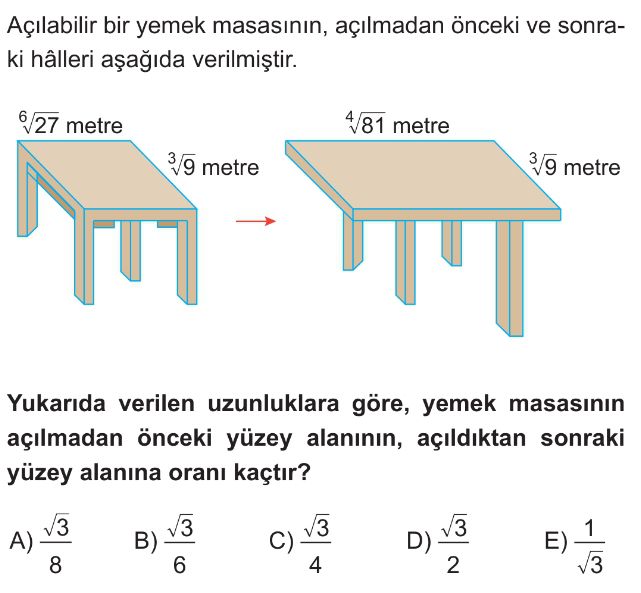
- Açılmadan önceki masanın uzun kenarını basitleştirelim: $^6\sqrt{27} = (3^3)^{1/6} = 3^{3/6} = 3^{1/2} = \sqrt{3}$ metre.
- Açılmadan önceki masanın kısa kenarını basitleştirelim: $^3\sqrt{9} = (3^2)^{1/3} = 3^{2/3}$ metre.
- Açılmadan önceki masanın yüzey alanı ($A_{önce}$): $A_{önce} = \sqrt{3} \cdot 3^{2/3}$ metrekare.
- Açıldıktan sonraki masanın uzun kenarını basitleştirelim: $^4\sqrt{81} = (3^4)^{1/4} = 3^{4/4} = 3^1 = 3$ metre.
- Açıldıktan sonraki masanın kısa kenarı aynıdır: $^3\sqrt{9} = (3^2)^{1/3} = 3^{2/3}$ metre.
- Açıldıktan sonraki masanın yüzey alanı ($A_{sonra}$): $A_{sonra} = 3 \cdot 3^{2/3}$ metrekare.
- Açılmadan önceki yüzey alanının, açıldıktan sonraki yüzey alanına oranını bulalım: $\frac{A_{önce}}{A_{sonra}} = \frac{\sqrt{3} \cdot 3^{2/3}}{3 \cdot 3^{2/3}}$.
- Oranı sadeleştirelim: $\frac{\sqrt{3}}{3} = \frac{3^{1/2}}{3^1} = 3^{1/2 - 1} = 3^{-1/2} = \frac{1}{3^{1/2}} = \frac{1}{\sqrt{3}}$.
- Doğru Seçenek E'dır.