Soru Çözümü
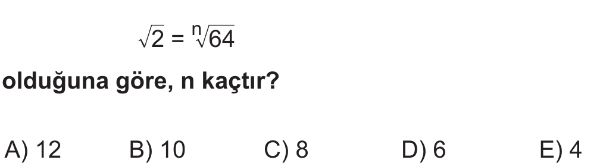
- Verilen denklemi `$\sqrt{2} = \sqrt[n]{64}$` olarak yazalım.
- Karekök `$\sqrt{2}$` ifadesini üslü olarak `$2^{1/2}$` şeklinde yazalım.
- `$64$` sayısını `$2^6$` olarak ifade edelim.
- `$\sqrt[n]{64}$` ifadesini üslü olarak `$(2^6)^{1/n}$` veya `$2^{6/n}$` şeklinde yazalım.
- Denklemi `$2^{1/2} = 2^{6/n}$` olarak yeniden düzenleyelim.
- Tabanlar eşit olduğundan, üsler de eşit olmalıdır: `$1/2 = 6/n$`.
- İçler dışlar çarpımı yaparak `$n \cdot 1 = 2 \cdot 6$` eşitliğini elde edelim.
- Buradan `$n = 12$` bulunur.
- Doğru Seçenek A'dır.