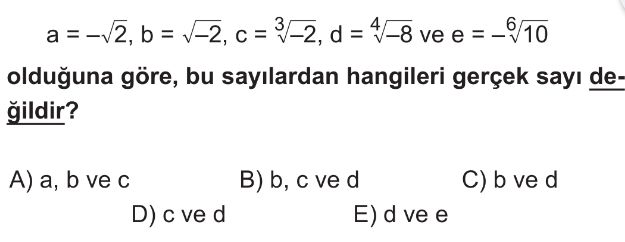
Soru Çözümü
- Bir köklü ifadenin (`$\sqrt[n]{x}$`) gerçek sayı olabilmesi için:
- Eğer kök derecesi (`$n$`) çift ise, kök içi (`$x$`) negatif olmamalıdır (`$x \ge 0$`).
- Eğer kök derecesi (`$n$`) tek ise, kök içi (`$x$`) herhangi bir gerçek sayı olabilir.
- `$a = -\sqrt{2}$`: Kök derecesi çift (2), kök içi pozitif (2). Gerçek sayıdır.
- `$b = \sqrt{-2}$`: Kök derecesi çift (2), kök içi negatif (-2). Gerçek sayı değildir.
- `$c = \sqrt[3]{-2}$`: Kök derecesi tek (3), kök içi negatif (-2). Gerçek sayıdır.
- `$d = \sqrt[4]{-8}$`: Kök derecesi çift (4), kök içi negatif (-8). Gerçek sayı değildir.
- `$e = -\sqrt[6]{10}$`: Kök derecesi çift (6), kök içi pozitif (10). Gerçek sayıdır.
- Gerçek sayı olmayanlar b ve d'dir.
- Doğru Seçenek C'dır.