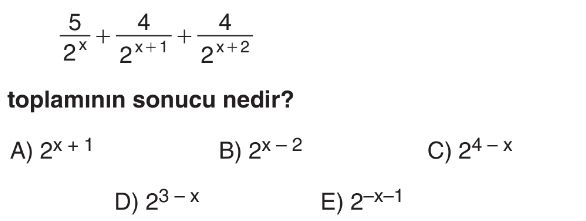
Soru Çözümü
- Verilen ifadeyi üslü sayı kurallarını kullanarak düzenleyelim.
- İkinci terimi basitleştirelim: $\frac{4}{2^{x+1}} = \frac{4}{2^x \cdot 2^1} = \frac{4}{2 \cdot 2^x} = \frac{2}{2^x}$
- Üçüncü terimi basitleştirelim: $\frac{4}{2^{x+2}} = \frac{4}{2^x \cdot 2^2} = \frac{4}{4 \cdot 2^x} = \frac{1}{2^x}$
- Şimdi ifadeyi yeniden yazalım: $\frac{5}{2^x} + \frac{2}{2^x} + \frac{1}{2^x}$
- Paydalar aynı olduğu için payları toplayalım: $\frac{5+2+1}{2^x} = \frac{8}{2^x}$
- $8$ sayısını $2$'nin kuvveti olarak yazalım: $8 = 2^3$
- İfadeyi yerine koyalım: $\frac{2^3}{2^x}$
- Üslü sayılar bölme kuralını uygulayalım ($a^m / a^n = a^{m-n}$): $2^{3-x}$
- Doğru Seçenek D'dır.