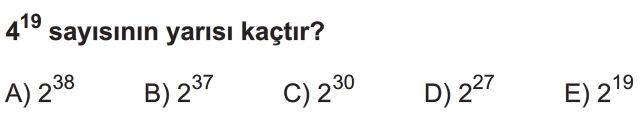
Soru Çözümü
- Verilen sayı $4^{19}$'dur.
- Öncelikle tabanı 2 cinsinden yazalım: $4 = 2^2$.
- Bu durumda $4^{19} = (2^2)^{19}$ olur.
- Üslü sayılarda kuvvetin kuvveti çarpılır: $(a^m)^n = a^{m \times n}$.
- Yani $ (2^2)^{19} = 2^{2 \times 19} = 2^{38} $.
- Sayının yarısını bulmak için 2'ye bölmemiz gerekir: $ \frac{2^{38}}{2} $.
- $2$ sayısı $2^1$ olarak ifade edilebilir.
- Üslü sayılarda bölme işleminde tabanlar aynıysa üsler çıkarılır: $ \frac{a^m}{a^n} = a^{m-n} $.
- Bu durumda $ \frac{2^{38}}{2^1} = 2^{38-1} = 2^{37} $.
- Doğru Seçenek B'dır.