Soru Çözümü
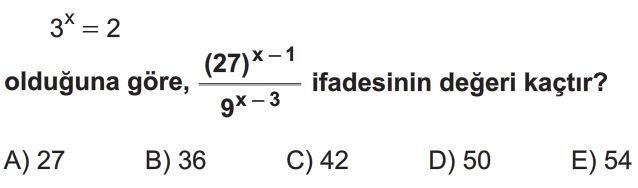
- Verilen ifadeyi basitleştirmek için 27 ve 9 sayılarını 3'ün kuvveti olarak yazalım: $27 = 3^3$ ve $9 = 3^2$.
- İfadeyi yerine yazalım: $\frac{(3^3)^{x-1}}{(3^2)^{x-3}}$.
- Üslü sayı kuralı $(a^m)^n = a^{mn}$ kullanarak üstleri çarpalım: $\frac{3^{3(x-1)}}{3^{2(x-3)}} = \frac{3^{3x-3}}{3^{2x-6}}$.
- Üslü sayı kuralı $\frac{a^m}{a^n} = a^{m-n}$ kullanarak üstleri çıkaralım: $3^{(3x-3)-(2x-6)} = 3^{3x-3-2x+6} = 3^{x+3}$.
- İfadeyi $3^{x+3} = 3^x \cdot 3^3$ şeklinde yazalım.
- Soruda verilen $3^x = 2$ değerini yerine koyalım: $2 \cdot 3^3$.
- $3^3 = 27$ olduğundan, ifade $2 \cdot 27 = 54$ olur.
- Doğru Seçenek E'dır.