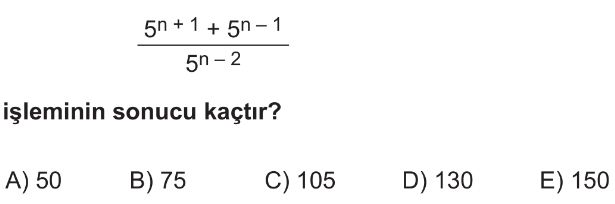
Soru Çözümü
- Verilen ifadeyi üslü sayı kurallarını kullanarak açalım: $5^{n+1} = 5^n \cdot 5^1$ ve $5^{n-1} = 5^n \cdot 5^{-1}$ ve $5^{n-2} = 5^n \cdot 5^{-2}$.
- İfadeyi bu şekilde yeniden yazalım: $\frac{5^n \cdot 5^1 + 5^n \cdot 5^{-1}}{5^n \cdot 5^{-2}}$.
- Pay kısmını $5^n$ parantezine alalım: $\frac{5^n (5^1 + 5^{-1})}{5^n \cdot 5^{-2}}$.
- Pay ve paydadaki $5^n$ terimlerini sadeleştirelim: $\frac{5^1 + 5^{-1}}{5^{-2}}$.
- Üslü ifadeleri sayı değerlerine çevirelim: $5^1 = 5$, $5^{-1} = \frac{1}{5}$, $5^{-2} = \frac{1}{25}$.
- İfadeyi yerine yazıp hesaplayalım: $\frac{5 + \frac{1}{5}}{\frac{1}{25}}$.
- Pay kısmını toplayalım: $5 + \frac{1}{5} = \frac{25}{5} + \frac{1}{5} = \frac{26}{5}$.
- Şimdi ifade $\frac{\frac{26}{5}}{\frac{1}{25}}$ haline geldi. Bölme işlemini çarpma işlemine çevirelim: $\frac{26}{5} \cdot 25$.
- Sadeleştirme yapalım: $26 \cdot \frac{25}{5} = 26 \cdot 5$.
- Sonucu bulalım: $26 \cdot 5 = 130$.
- Doğru Seçenek D'dır.