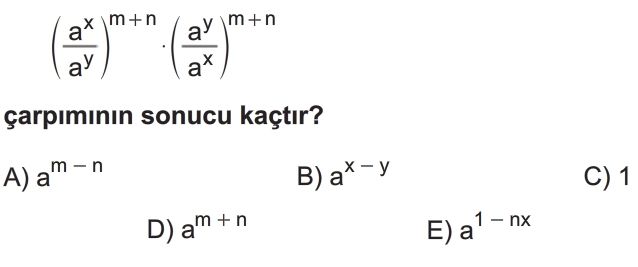
Soru Çözümü
- Verilen ifadeyi üslü sayılar kurallarına göre düzenleyelim: `$ (\frac{a^x}{a^y})^{m+n} \cdot (\frac{a^y}{a^x})^{m+n} $`
- Parantez içindeki ifadeleri `$ \frac{a^p}{a^q} = a^{p-q} $` kuralını kullanarak sadeleştirelim:
- İlk parantez: `$ \frac{a^x}{a^y} = a^{x-y} $`
- İkinci parantez: `$ \frac{a^y}{a^x} = a^{y-x} $`
- İfade `$ (a^{x-y})^{m+n} \cdot (a^{y-x})^{m+n} $` haline gelir.
- Üssün üssü kuralını `$ (a^p)^q = a^{pq} $` uygulayalım:
- İlk terim: `$ a^{(x-y)(m+n)} $`
- İkinci terim: `$ a^{(y-x)(m+n)} $`
- Şimdi bu iki terimi çarpalım: `$ a^{(x-y)(m+n)} \cdot a^{(y-x)(m+n)} $`
- Tabanlar aynı olduğu için üsleri toplayalım: `$ a^{(x-y)(m+n) + (y-x)(m+n)} $`
- Üs ifadesinde `$ (m+n) $` ortak çarpanını dışarı alalım: `$ a^{(m+n)[(x-y) + (y-x)]} $`
- Köşeli parantez içindeki ifadeyi sadeleştirelim: `$ (x-y) + (y-x) = x-y+y-x = 0 $`
- Üs `$ (m+n) \cdot 0 = 0 $` olur.
- Sonuç `$ a^0 $` olur.
- Sıfır hariç herhangi bir sayının sıfırıncı kuvveti 1'dir: `$ a^0 = 1 $`
- Doğru Seçenek C'dır.