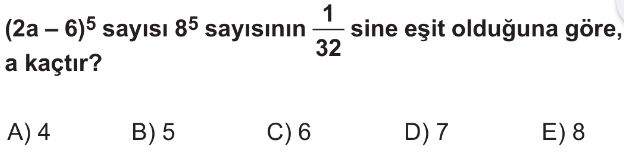
Soru Çözümü
- Verilen denklemi yazalım: $(2a - 6)^5 = 8^5 \cdot \frac{1}{32}$
- $8^5$ ifadesini $2$ tabanında yazalım: $8^5 = (2^3)^5 = 2^{15}$
- $\frac{1}{32}$ ifadesini $2$ tabanında yazalım: $\frac{1}{32} = \frac{1}{2^5} = 2^{-5}$
- Denklemin sağ tarafını düzenleyelim: $2^{15} \cdot 2^{-5} = 2^{15-5} = 2^{10}$
- Denklem şimdi şu şekildedir: $(2a - 6)^5 = 2^{10}$
- $2^{10}$ ifadesini $5$. kuvvet olarak yazalım: $2^{10} = (2^2)^5 = 4^5$
- Denklem şu hale gelir: $(2a - 6)^5 = 4^5$
- Üsler eşit ve tek sayı olduğu için tabanlar da eşittir: $2a - 6 = 4$
- $2a = 4 + 6$
- $2a = 10$
- $a = \frac{10}{2}$
- $a = 5$
- Doğru Seçenek B'dır.