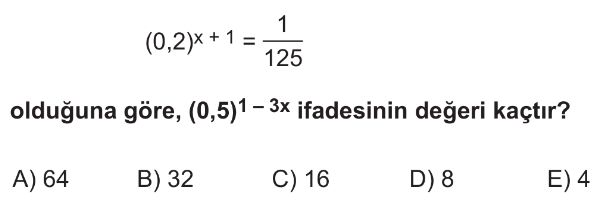
Soru Çözümü
- Verilen denklemi düzenleyelim: $(0,2)^{x+1} = \frac{1}{125}$
- Ondalık sayıları ve kesirleri üslü ifade olarak yazalım: $0,2 = \frac{2}{10} = \frac{1}{5} = 5^{-1}$ ve $\frac{1}{125} = \frac{1}{5^3} = 5^{-3}$
- Denklemde yerine yazalım: $(5^{-1})^{x+1} = 5^{-3}$
- Üsleri çarpalım: $5^{-(x+1)} = 5^{-3} \implies 5^{-x-1} = 5^{-3}$
- Tabanlar aynı olduğu için üsleri eşitleyelim: $-x-1 = -3 \implies -x = -2 \implies x = 2$
- Şimdi bizden istenen $(0,5)^{1-3x}$ ifadesinin değerini bulalım.
- $0,5$ sayısını kesir olarak yazalım: $0,5 = \frac{5}{10} = \frac{1}{2}$
- $x=2$ değerini $1-3x$ üssüne yerine yazalım: $1-3(2) = 1-6 = -5$
- İfadeyi yerine yazalım: $(\frac{1}{2})^{-5}$
- Üslü ifadeyi hesaplayalım: $(\frac{1}{2})^{-5} = (2^{-1})^{-5} = 2^{(-1) \cdot (-5)} = 2^5 = 32$
- Doğru Seçenek B'dır.