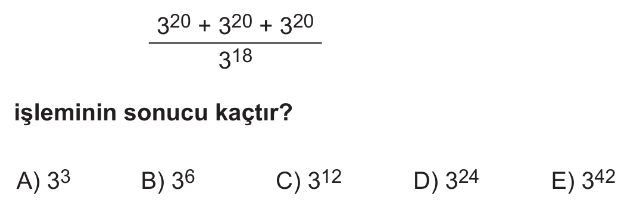
Soru Çözümü
- Pay kısmındaki $3^{20} + 3^{20} + 3^{20}$ ifadesi, $3$ tane $3^{20}$ anlamına gelir. Bu ifadeyi $3 \cdot 3^{20}$ olarak yazabiliriz.
- Üslü sayılarda çarpma kuralına göre ($a^m \cdot a^n = a^{m+n}$), $3 \cdot 3^{20}$ ifadesi $3^1 \cdot 3^{20} = 3^{1+20} = 3^{21}$ olur.
- İşlemimiz şimdi $\frac{3^{21}}{3^{18}}$ şeklini aldı.
- Üslü sayılarda bölme kuralına göre ($\frac{a^m}{a^n} = a^{m-n}$), bu ifade $3^{21-18}$ olarak yazılır.
- Üsleri çıkarırsak $21-18 = 3$ bulunur. Yani sonuç $3^3$'tür.
- Doğru Seçenek A'dır.