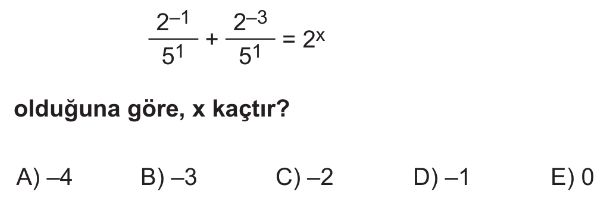
Soru Çözümü
- Verilen denklem: $\frac{2^{-1}}{5^1} + \frac{2^{-3}}{5^1} = 2^x$
- Üslü ifadeleri basitleştirelim: $2^{-1} = \frac{1}{2}$ ve $2^{-3} = \frac{1}{8}$
- Denklemde yerine yazalım: $\frac{\frac{1}{2}}{5} + \frac{\frac{1}{8}}{5} = 2^x$
- Kesirleri düzenleyelim: $\frac{1}{2 \cdot 5} + \frac{1}{8 \cdot 5} = 2^x \Rightarrow \frac{1}{10} + \frac{1}{40} = 2^x$
- Paydaları eşitleyelim (ortak payda 40): $\frac{4}{40} + \frac{1}{40} = 2^x$
- Toplama işlemini yapalım: $\frac{4+1}{40} = 2^x \Rightarrow \frac{5}{40} = 2^x$
- Kesri sadeleştirelim: $\frac{1}{8} = 2^x$
- $\frac{1}{8}$ ifadesini 2'nin kuvveti olarak yazalım: $\frac{1}{2^3} = 2^{-3}$
- Denklemi tekrar yazalım: $2^{-3} = 2^x$
- Tabanlar eşit olduğu için üsler de eşit olmalıdır: $x = -3$
- Doğru Seçenek B'dır.