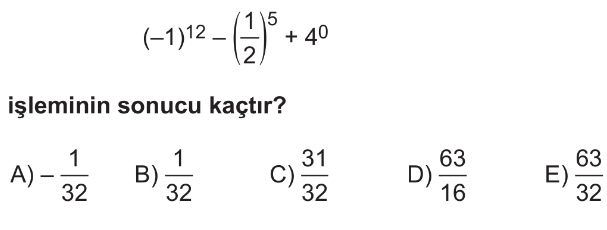
Soru Çözümü
- İlk olarak, verilen ifadeyi oluşturan terimleri ayrı ayrı hesaplayalım.
- $(-1)^{12}$ ifadesinin değeri, negatif bir sayının çift kuvveti pozitif olacağından $1$'dir.
- $(\frac{1}{2})^5$ ifadesinin değeri, pay ve paydanın ayrı ayrı 5. kuvveti alınarak $\frac{1^5}{2^5} = \frac{1}{32}$ olarak bulunur.
- $4^0$ ifadesinin değeri, sıfırdan farklı bir sayının 0. kuvveti 1 olduğundan $1$'dir.
- Şimdi bu değerleri ana ifadede yerine yazalım: $1 - \frac{1}{32} + 1$.
- Tam sayıları toplayalım: $1 + 1 - \frac{1}{32} = 2 - \frac{1}{32}$.
- İfadeyi ortak paydaya getirerek çıkarma işlemini yapalım: $2 = \frac{64}{32}$.
- Sonuç olarak, $\frac{64}{32} - \frac{1}{32} = \frac{64 - 1}{32} = \frac{63}{32}$ elde edilir.
- Doğru Seçenek E'dır.