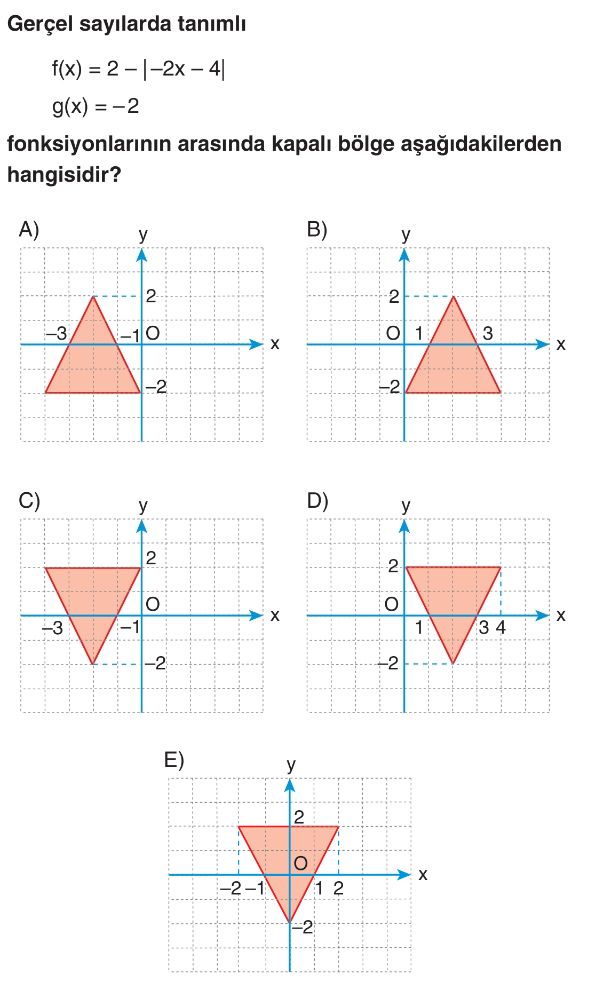
Soru Çözümü
- Verilen fonksiyonlar $f(x) = 2 - |-2x - 4|$ ve $g(x) = -2$'dir.
- Öncelikle $f(x)$ fonksiyonunu basitleştirelim: $f(x) = 2 - |-(2x + 4)| = 2 - |2x + 4|$.
- $f(x)$ fonksiyonunun tepe noktasını bulalım. Mutlak değerin içini sıfır yapan $x$ değeri için $2x + 4 = 0 \Rightarrow 2x = -4 \Rightarrow x = -2$.
- Bu $x$ değeri için $f(-2) = 2 - |2(-2) + 4| = 2 - |0| = 2$. Yani tepe noktası $(-2, 2)$'dir.
- Kapalı bölgeyi oluşturan diğer noktaları bulmak için $f(x)$ ve $g(x)$ fonksiyonlarını eşitleyelim: $2 - |2x + 4| = -2$.
- Mutlak değeri yalnız bırakalım: $|2x + 4| = 2 + 2 \Rightarrow |2x + 4| = 4$.
- İki durum oluşur:
- $2x + 4 = 4 \Rightarrow 2x = 0 \Rightarrow x = 0$. Bu nokta $(0, -2)$'dir.
- $2x + 4 = -4 \Rightarrow 2x = -8 \Rightarrow x = -4$. Bu nokta $(-4, -2)$'dir.
- Buna göre, kapalı bölge bir üçgendir ve köşeleri $(-2, 2)$, $(-4, -2)$ ve $(0, -2)$ noktalarıdır.
- Seçeneklere baktığımızda, A seçeneğindeki grafik bu üçgeni doğru şekilde göstermektedir. Tepe noktası $(-2, 2)$, tabanı $y = -2$ doğrusu üzerinde ve $x = -4$ ile $x = 0$ noktalarında kesişmektedir.
- Doğru Seçenek A'dır.