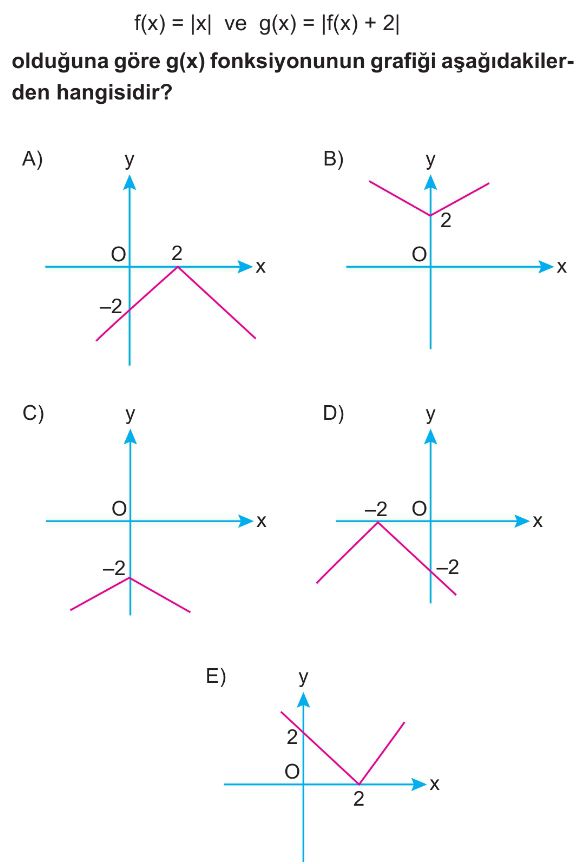
Soru Çözümü
- Verilen fonksiyonlar $f(x) = |x|$ ve $g(x) = |f(x) + 2|$'dir.
- $f(x)$ ifadesini $g(x)$ yerine koyarsak, $g(x) = ||x| + 2|$ elde ederiz.
- Mutlak değerin içindeki ifadeye bakalım: $|x| + 2$.
- $|x| \ge 0$ olduğu için, $|x| + 2 \ge 2$ olur. Yani mutlak değerin içi her zaman pozitiftir.
- Bu durumda, $||x| + 2| = |x| + 2$ olur.
- $g(x) = |x| + 2$ fonksiyonunun grafiği, $f(x) = |x|$ grafiğinin y ekseninde $2$ birim yukarı ötelenmiş halidir.
- $f(x) = |x|$ grafiğinin tepe noktası $(0,0)$ iken, $g(x) = |x| + 2$ grafiğinin tepe noktası $(0,2)$ olur ve yukarı doğru açılır.
- Bu özelliklere sahip grafik B seçeneğinde gösterilmiştir.
- Doğru Seçenek B'dır.