Soru Çözümü
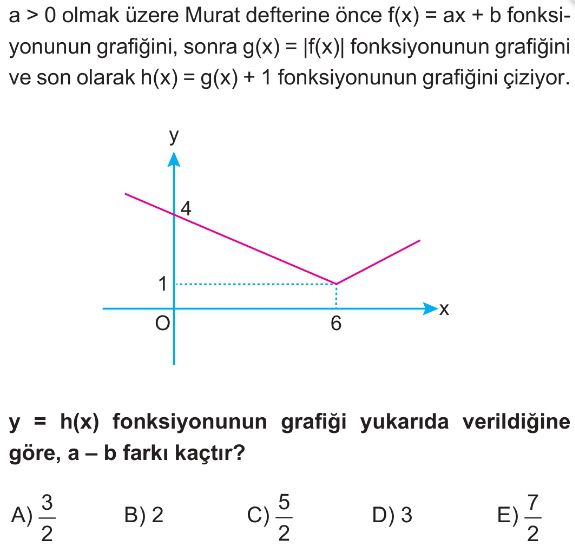
- Verilen $h(x)$ grafiğinden noktaları belirleyelim. Grafiğe göre $h(0) = 4$ ve $h(6) = 1$.
- $h(x) = g(x) + 1$ bağıntısını kullanarak $g(x)$ değerlerini bulalım. $g(x) = h(x) - 1$ olur.
- Buna göre $g(0) = h(0) - 1 = 4 - 1 = 3$ ve $g(6) = h(6) - 1 = 1 - 1 = 0$ bulunur.
- $g(x) = |f(x)|$ olduğu için $|f(0)| = 3$ ve $|f(6)| = 0$ olur.
- $|f(6)| = 0$ eşitliğinden $f(6) = 0$ sonucuna ulaşırız.
- $f(x) = ax + b$ fonksiyonunda $f(6) = 0$ ise $a(6) + b = 0 \Rightarrow 6a + b = 0$.
- Soruda $a > 0$ verildiği için $f(x)$ fonksiyonu artan bir fonksiyondur.
- $f(x)$ artan ve $f(6) = 0$ ise, $x < 6$ için $f(x) < 0$ olmalıdır. Dolayısıyla $f(0) < 0$.
- $|f(0)| = 3$ ve $f(0) < 0$ olduğundan $f(0) = -3$ olmalıdır.
- $f(x) = ax + b$ fonksiyonunda $x=0$ için $f(0) = a(0) + b = b$ olduğundan $b = -3$.
- $6a + b = 0$ denkleminde $b = -3$ yerine yazılırsa $6a - 3 = 0 \Rightarrow 6a = 3 \Rightarrow a = 1/2$.
- Son olarak $a - b$ farkını hesaplayalım: $a - b = 1/2 - (-3) = 1/2 + 3 = 1/2 + 6/2 = 7/2$.
- Doğru Seçenek E'dır.