Soru Çözümü
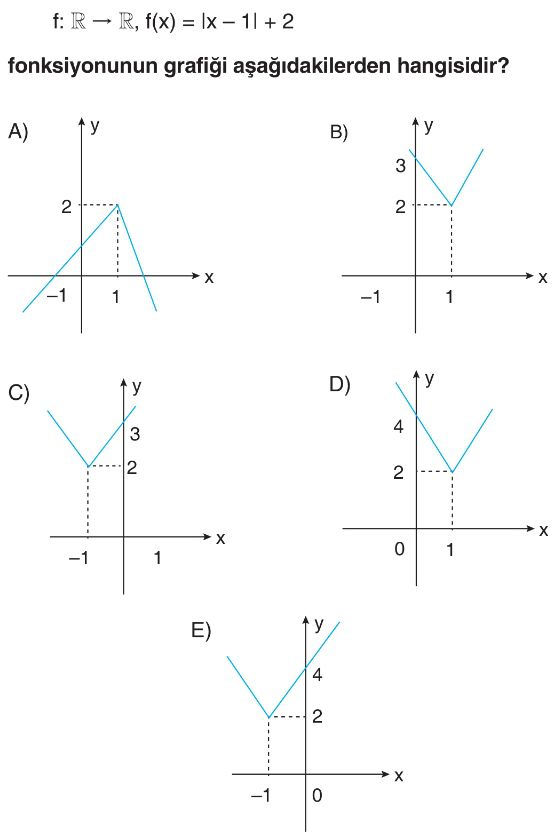
- Verilen fonksiyon $f(x) = |x - 1| + 2$'dir.
- Mutlak değer fonksiyonlarının genel formu $y = |x - h| + k$ olduğunda, grafiğin tepe noktası $(h, k)$'dir.
- Bu fonksiyonda $h = 1$ ve $k = 2$ olduğundan, grafiğin tepe noktası $(1, 2)$'dir.
- Seçeneklere baktığımızda, tepe noktası $(1, 2)$ olan grafikler B ve D seçenekleridir.
- Grafiğin y eksenini kestiği noktayı bulmak için $x = 0$ değerini fonksiyonda yerine koyalım: $f(0) = |0 - 1| + 2 = |-1| + 2 = 1 + 2 = 3$.
- Bu durumda, grafik $(0, 3)$ noktasından geçmelidir.
- B seçeneğindeki grafik $(1, 2)$ tepe noktasına sahiptir ve y eksenini $(0, 3)$ noktasında keser.
- D seçeneğindeki grafik $(1, 2)$ tepe noktasına sahiptir ancak y eksenini $(0, 4)$ noktasında keser.
- Bu bilgilere göre, doğru grafik B seçeneğidir.
- Doğru Seçenek B'dır.