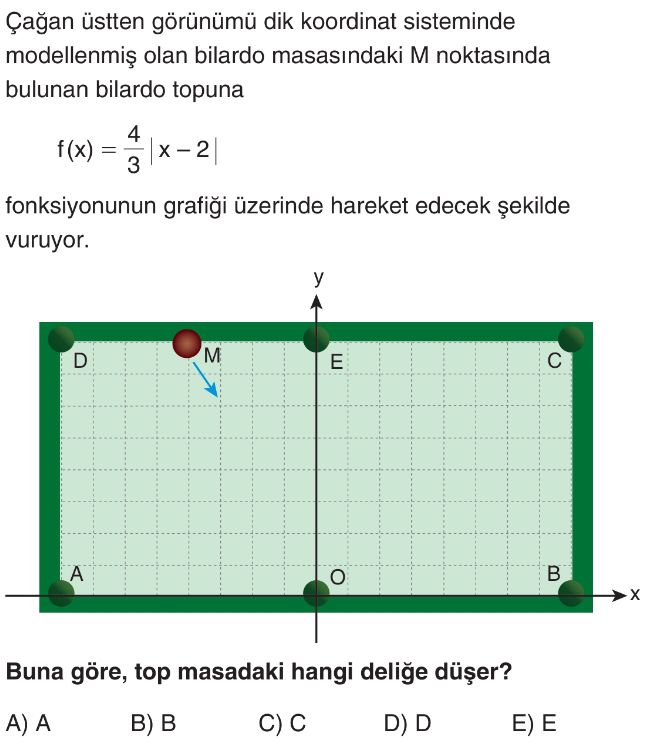
Soru Çözümü
- Verilen fonksiyon $f(x) = \frac{4}{3}|x - 2|$'dir. Bu fonksiyonun tepe noktası, mutlak değerin içini sıfır yapan $x$ değeri için $x-2=0 \implies x=2$'dir. Bu durumda $f(2)=0$ olur. Yani tepe noktası $(2, 0)$'dır.
- Şekildeki koordinat sistemine göre $(2, 0)$ noktası B deliğine karşılık gelir.
- Topun başlangıç noktası M'dir. Şekilden M noktasının koordinatları $(-1, 4)$ olarak okunur. Fonksiyonda $x=-1$ yazarsak $f(-1) = \frac{4}{3}|-1 - 2| = \frac{4}{3}|-3| = \frac{4}{3} \times 3 = 4$ bulunur. Bu da M noktasının fonksiyon üzerinde olduğunu gösterir.
- Ok işareti, topun M noktasından başlayıp $x$ değerleri artacak şekilde hareket ettiğini gösterir. Bu durumda top, $x=-1$ noktasından başlayarak tepe noktası olan $(2, 0)$'a (B deliğine) doğru ilerleyecektir.
- Top B deliğinden geçtikten sonra fonksiyonun diğer dalı üzerinde hareket etmeye devam edecektir. Fonksiyonun $x > 2$ için dalı $f(x) = \frac{4}{3}(x - 2)$'dir. Masadaki deliklerden C noktasının koordinatları şekilden $(5, 4)$ olarak okunur.
- $x=5$ için fonksiyon değerini hesaplayalım: $f(5) = \frac{4}{3}|5 - 2| = \frac{4}{3}|3| = \frac{4}{3} \times 3 = 4$. Bu da C noktasının $(5, 4)$ fonksiyon üzerinde olduğunu gösterir.
- Dolayısıyla top, M noktasından başlayıp B deliğinden geçerek C deliğine düşer.
- Doğru Seçenek C'dır.