Soru Çözümü
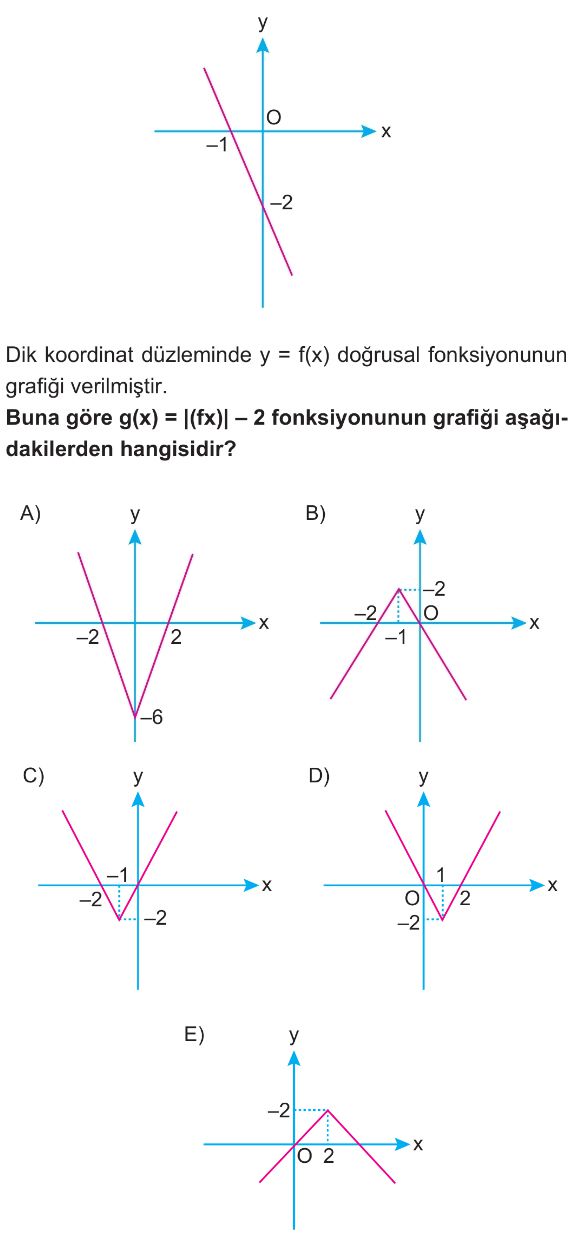
- Verilen $f(x)$ fonksiyonunun grafiği x eksenini $(-1, 0)$ noktasında, y eksenini $(0, -2)$ noktasında keser. Bu bilgilere göre $f(x)$'in denklemi $f(x) = -2x - 2$'dir.
- $|f(x)|$ fonksiyonunun grafiği, $f(x)$'in x ekseninin altında kalan kısmının x eksenine göre yansıtılmasıyla elde edilir. $f(x)=0$ için $x=-1$ olduğundan, $|f(x)|$ grafiğinin tepe noktası $(-1, 0)$ olur. $x=0$ için $|f(0)| = |-2| = 2$ olduğundan y eksenini $(0, 2)$ noktasında keser.
- $g(x) = |f(x)| - 2$ fonksiyonunun grafiği, $|f(x)|$ grafiğinin 2 birim aşağı ötelenmesiyle elde edilir.
- Bu öteleme sonucunda:
- Tepe noktası $(-1, 0)$ noktasından $(-1, 0 - 2) = (-1, -2)$ noktasına kayar.
- Y eksenini kestiği nokta $(0, 2)$ noktasından $(0, 2 - 2) = (0, 0)$ noktasına kayar. Yani orijinden geçer.
- x eksenini kestiği noktaları bulmak için $g(x) = 0$ denklemini çözeriz: $|f(x)| - 2 = 0 \Rightarrow |f(x)| = 2$.
- $-2x - 2 = 2 \Rightarrow -2x = 4 \Rightarrow x = -2$.
- $-2x - 2 = -2 \Rightarrow -2x = 0 \Rightarrow x = 0$.
- Tepe noktası $(-1, -2)$ olan, x eksenini $(-2, 0)$ ve $(0, 0)$ noktalarında kesen grafik C seçeneğinde gösterilmiştir.
- Doğru Seçenek C'dır.