Soru Çözümü
- Verilen fonksiyon $f(x) = |3x - 6| + 1$ şeklindedir.
- Mutlak değerin içini sıfır yapan $x$ değerini bulalım: $3x - 6 = 0 \Rightarrow 3x = 6 \Rightarrow x = 2$.
- Bu $x$ değeri, fonksiyonun grafiğinin "köşe" noktasının apsisidir. Fonksiyonun bu noktadaki değerini bulalım: $f(2) = |3(2) - 6| + 1 = |6 - 6| + 1 = |0| + 1 = 1$.
- Yani, grafiğin minimum noktası $(2, 1)$ koordinatındadır.
- Şimdi y eksenini kestiği noktayı bulalım. Bunun için $x = 0$ değerini fonksiyonda yerine yazalım: $f(0) = |3(0) - 6| + 1 = |-6| + 1 = 6 + 1 = 7$.
- Grafik y eksenini $(0, 7)$ noktasında keser.
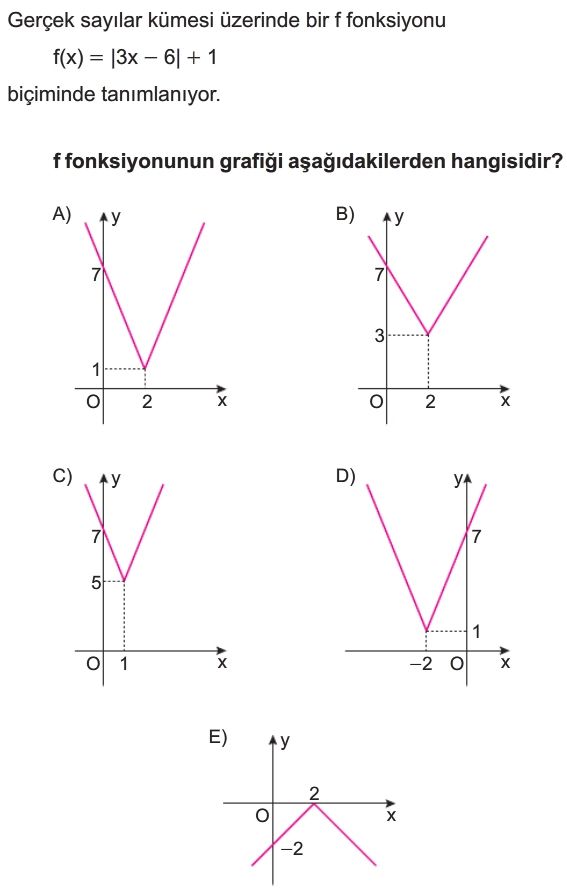
- Bu bilgilere göre, minimum noktası $(2, 1)$ olan ve y eksenini $(0, 7)$ noktasında kesen grafik A seçeneğinde verilmiştir.
- Doğru Seçenek A'dır.