Soru Çözümü
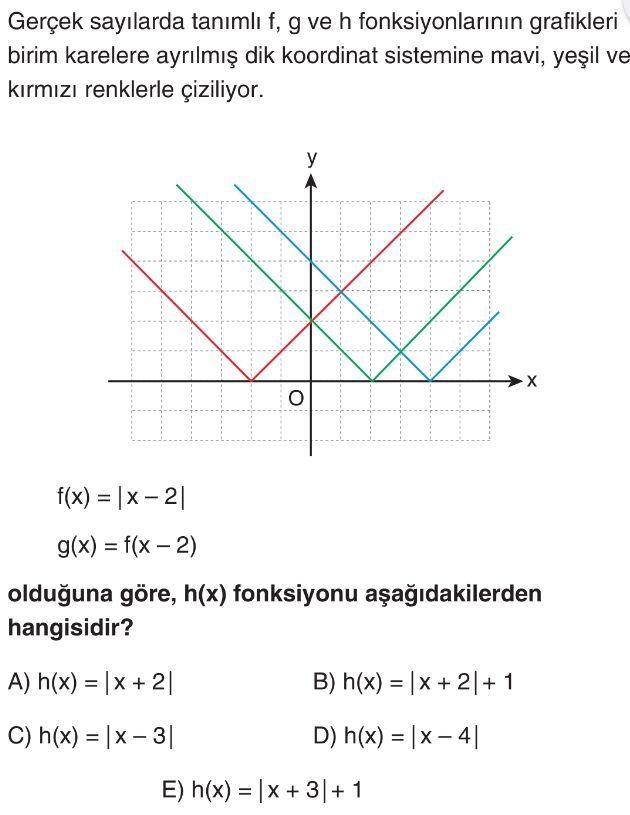
- Verilen $f(x) = |x - 2|$ fonksiyonunun grafiği, tepe noktası $(2, 0)$ olan V şeklindedir. Grafikteki mavi çizgi bu tanıma uyar, yani $f(x)$ mavi grafiktir.
- $g(x) = f(x - 2)$ fonksiyonunu bulalım. $f(x - 2) = |(x - 2) - 2| = |x - 4|$. Bu fonksiyonun grafiği, tepe noktası $(4, 0)$ olan V şeklindedir. Grafikteki yeşil çizgi bu tanıma uyar, yani $g(x)$ yeşil grafiktir.
- Geriye kalan kırmızı çizgi $h(x)$ fonksiyonunun grafiğidir. Kırmızı grafiğin tepe noktası $(-2, 0)$ noktasındadır.
- Tepe noktası $(-2, 0)$ olan mutlak değer fonksiyonu $h(x) = |x - (-2)| = |x + 2|$ şeklindedir.
- Doğru Seçenek A'dır.