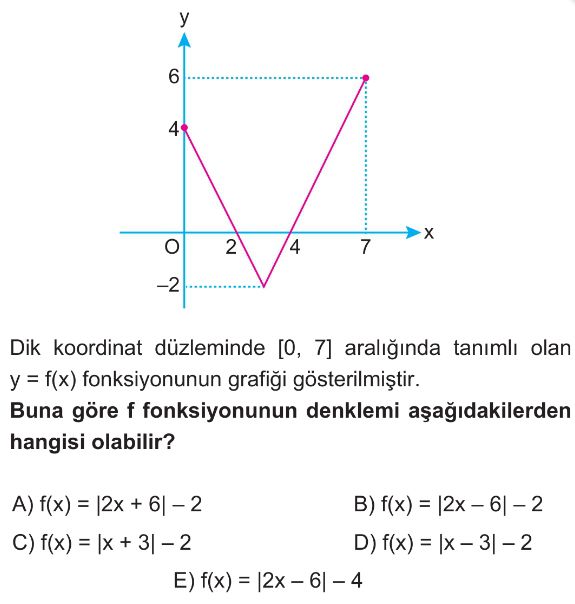
Soru Çözümü
- Grafiğin tepe noktası (minimum noktası) $(3, -2)$'dir.
- Mutlak değer fonksiyonunun genel formu $f(x) = a|x - h| + k$ olduğundan, tepe noktası $(h, k) = (3, -2)$ için fonksiyon $f(x) = a|x - 3| - 2$ şeklindedir.
- Grafik $(0, 4)$ noktasından geçtiği için bu noktayı fonksiyonda yerine yazalım: $4 = a|0 - 3| - 2$ $4 = a|-3| - 2$ $4 = 3a - 2$ $6 = 3a$ $a = 2$
- Buna göre fonksiyonun denklemi $f(x) = 2|x - 3| - 2$ olur.
- Şimdi seçenekleri kontrol edelim. B seçeneği $f(x) = |2x - 6| - 2$ olarak verilmiştir. Mutlak değerin içindeki $2$ çarpanını dışarı alırsak: $|2x - 6| = |2(x - 3)| = |2||x - 3| = 2|x - 3|$ Böylece B seçeneği $f(x) = 2|x - 3| - 2$ olur.
- Bu denklem, grafikten elde ettiğimiz denklemle aynıdır.
- Doğru Seçenek B'dır.