Soru Çözümü
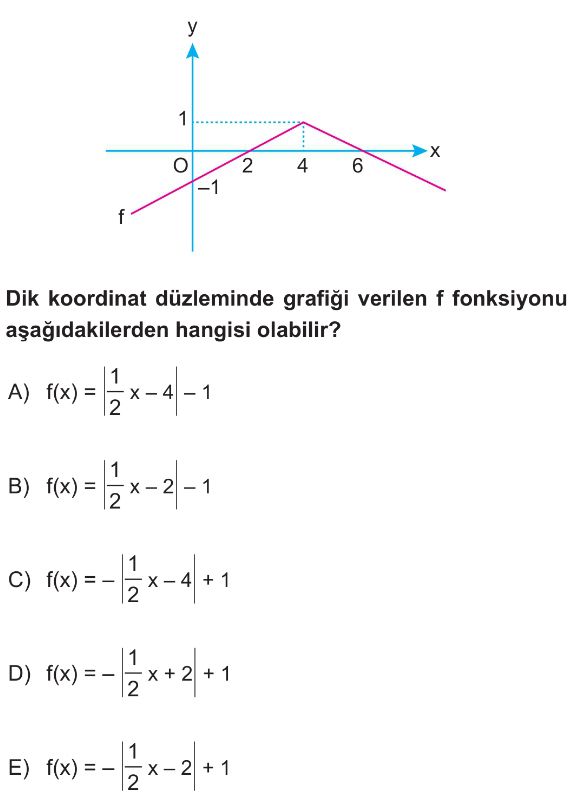
- Verilen grafik bir mutlak değer fonksiyonunun grafiğidir ve "V" şeklindedir. Grafik aşağı doğru açıldığı için mutlak değerin önündeki katsayı negatif olmalıdır. Bu durum A ve B seçeneklerini eler.
- Grafiğin tepe noktası (köşe noktası) $(2, 1)$'dir.
- Genel mutlak değer fonksiyonu $f(x) = a|x-h| + k$ şeklinde olup, tepe noktası $(h, k)$'dir. Grafiğimizde tepe noktası $(2, 1)$ olduğundan, fonksiyon $f(x) = a|x-2| + 1$ formunda olmalıdır.
- Kalan seçeneklerden C, D ve E'yi inceleyelim:
- C) $f(x) = -\frac{1}{2}|x - 4| + 1$: Tepe noktası $(4, 1)$'dir. Grafiğe uymaz.
- D) $f(x) = -\frac{1}{2}|x + 2| + 1$: Tepe noktası $(-2, 1)$'dir. Grafiğe uymaz.
- E) $f(x) = -\frac{1}{2}|x - 2| + 1$: Tepe noktası $(2, 1)$'dir. Bu, grafiğin tepe noktası ile eşleşir.
- E seçeneğindeki fonksiyonu grafikteki başka bir nokta ile kontrol edelim. Örneğin, grafik $(0, 0)$ noktasından geçmektedir. $f(0) = -\frac{1}{2}|0 - 2| + 1 = -\frac{1}{2}|-2| + 1 = -\frac{1}{2}(2) + 1 = -1 + 1 = 0$. Bu nokta fonksiyona uymaktadır.
- Doğru Seçenek E'dır.