Soru Çözümü
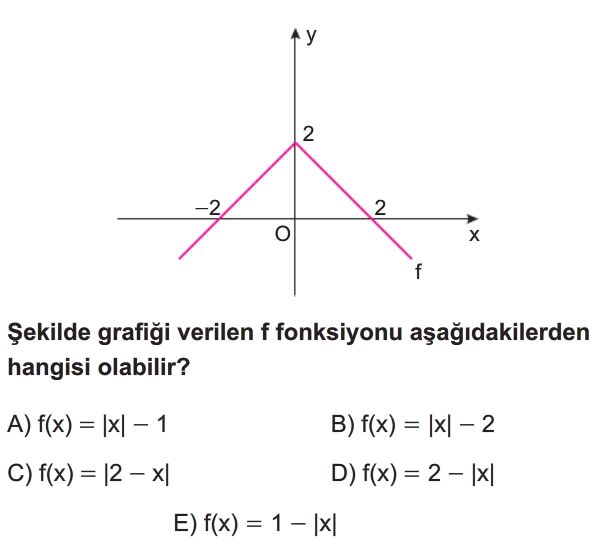
- Grafikte verilen fonksiyonun tepe noktası $(0, 2)$'dir. Yani $x=0$ için $f(x)=2$ olmalıdır.
- Grafik x eksenini $(-2, 0)$ ve $(2, 0)$ noktalarında kesmektedir. Yani $f(-2)=0$ ve $f(2)=0$ olmalıdır.
- Seçenekleri kontrol edelim:
- A) $f(x) = |x| - 1 \implies f(0) = |0| - 1 = -1$. Tepe noktası uymuyor.
- B) $f(x) = |x| - 2 \implies f(0) = |0| - 2 = -2$. Tepe noktası uymuyor.
- C) $f(x) = |2 - x| \implies f(0) = |2 - 0| = 2$. Tepe noktası uyuyor. Ancak $f(-2) = |2 - (-2)| = |4| = 4 \ne 0$. x-kesişimi uymuyor.
- D) $f(x) = 2 - |x|$
- $f(0) = 2 - |0| = 2 - 0 = 2$. Tepe noktası $(0, 2)$ uyuyor.
- $f(2) = 2 - |2| = 2 - 2 = 0$. x-kesişimi $(2, 0)$ uyuyor.
- $f(-2) = 2 - |-2| = 2 - 2 = 0$. x-kesişimi $(-2, 0)$ uyuyor.
- Bu fonksiyonun grafiği verilen grafikle tamamen eşleşmektedir.
- E) $f(x) = 1 - |x| \implies f(0) = 1 - |0| = 1$. Tepe noktası uymuyor.
- Doğru Seçenek D'dır.