Soru Çözümü
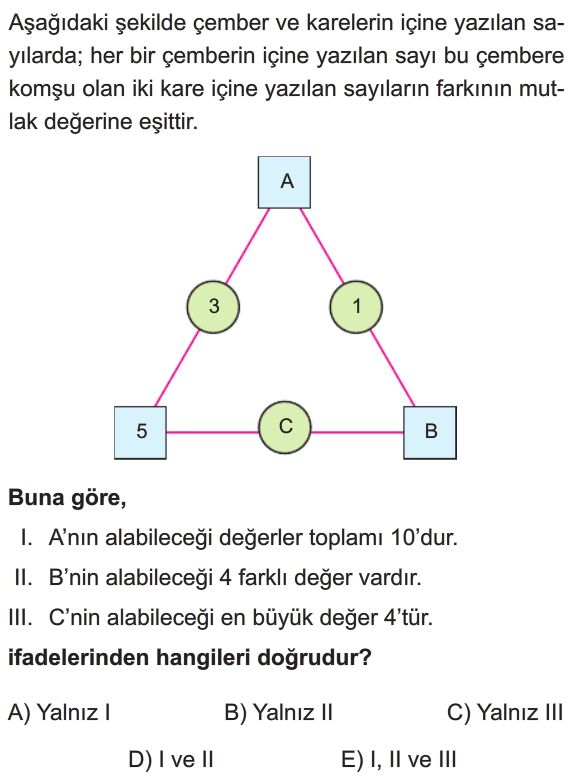
- Verilen kurala göre, her bir çemberdeki sayı komşu karelerdeki sayıların farkının mutlak değeridir.
- Çember 3 için: $|A - 5| = 3$.
Bu durumda $A - 5 = 3$ veya $A - 5 = -3$ olur.
$A = 8$ veya $A = 2$. - I. İfade: A'nın alabileceği değerler toplamı $8 + 2 = 10$'dur. Bu ifade doğrudur.
- Çember 1 için: $|A - B| = 1$.
- Eğer $A = 8$ ise, $|8 - B| = 1$.
$8 - B = 1 \Rightarrow B = 7$ veya $8 - B = -1 \Rightarrow B = 9$. - Eğer $A = 2$ ise, $|2 - B| = 1$.
$2 - B = 1 \Rightarrow B = 1$ veya $2 - B = -1 \Rightarrow B = 3$.
- Eğer $A = 8$ ise, $|8 - B| = 1$.
- II. İfade: B'nin alabileceği değerler $1, 3, 7, 9$'dur. Toplam 4 farklı değer vardır. Bu ifade doğrudur.
- Çember C için: $C = |5 - B|$.
- $B = 1$ için $C = |5 - 1| = 4$.
- $B = 3$ için $C = |5 - 3| = 2$.
- $B = 7$ için $C = |5 - 7| = |-2| = 2$.
- $B = 9$ için $C = |5 - 9| = |-4| = 4$.
- III. İfade: C'nin alabileceği değerler $2$ ve $4$'tür. C'nin alabileceği en büyük değer $4$'tür. Bu ifade doğrudur.
- Tüm ifadeler (I, II ve III) doğrudur.
- Doğru Seçenek E'dır.